Auxiliary AMG Preconditioner for H(div) systems

AUXILIARY AMG PRECONDITIONER FOR H(div) SYSTEMS

YUNRONG ZHU

1. Problem description

This package is to solve the following H(div) system, by using varies auxiliary AMG preconditioners. The goal is to verify the efficiency and robustness of these preconditioners with respect to different coefficients of ϵ > 0 on unstructured mesh.

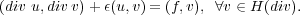(div u,div v)+ ϵ(u,v) = (f,v), ∀v ∈ H(div).

(1.1)

Let the domain Ω = [0,1]³ be the unit cube. It is triangulated by unstructured tetrahedron mesh. We consider the finite element discretization of equation (1.1) by lowest order Raviart-Thomas element. Three sample unstructured data sets of the mesh are given in mesh*.dat files. The data files *.mat are the corresponding stiffness and mass matrices related to mesh*.dat.

mesh8.mat 8.mat: The data files for the unstructured mesh with 8 intervals in each direction. The total number of degree of freedoms (number of faces) is 8,924.
mesh16.mat 16.mat: The data files for the unstructured mesh with 16 intervals in each direction. The total number of degree of freedoms (number of faces) is 71,882.
mesh26.mat 26.mat: The data files for the unstructured mesh with 26 intervals in each direction. The total number of degree of freedoms (number of faces) is 305,508.

Click here for a full description of the source codes, to download of the codes and data files, as well as the performance of the algorithms.

4. Some Useful Matlab Subroutines

mesh3dT.m: It generates a 3D structured tetrahedron patition of the unit cube.
cg4.m: A conjugate gradient subroutine by Chris Siefert.
load_coordinates.m: Itloads the coordinates data of the mesh from an ASCII file.
load_elements.m: It loads the element data of the mesh from an ASCII file.