Chapter 12 R and Your Computer
“Those who can imagine anything, can create the impossible.”
- Alan Turing, (1912–1954)
12.1 How Do Computers Work?
To better understand R we need to understand the underlying constraints of computer systems we use to run R. Computers accept data, process data, produce output, and store processed results. This is generally accomplished through through the generation, integration and storage of electrical signals at microscopic scales. A list of (current but often changing) computer hardware terms are given below.
Power supply: Converts alternating current (AC) electric power to low-voltage direct current (DC) power.
Motherboard: A circuit board connecting computer components including the CPU, RAM and memory disk drives.
Central Processing Unit (CPU): A microprocessor that performs most of the calculations that allow a computer to function. Specifically, the CPU processes program instructions and sends the results on for further processing and execution by other computer components.
Graphics Processing Unit (GPU): An electronic circuit originally designed to accelerate computer graphics, but now widely applied for non-graphic, but highly parallel, calculations.
Chipset: Mediates communication between the CPU and the other computer components.
Random Access Memory (RAM): Stores code and data in primary memory to allow it to be directly accessed by the CPU. RAM is volatile memory which requires power to retain stored information. Thus, when power is interrupted, RAM data can be lost. RAM types include dynamic random access memory (DRAM) and static random-access memory (SRAM). DRAM constitutes modern computer main memory and graphics cards. DRAM typically takes the form of an integrated circuit chip that can consist of up to billions of memory cells, with each cell consisting of a pairing of a tiny capacitor1 and transistor2, allowing each cell to store or read or write one bit of information (Fig 12.1). SRAM uses latching circuitry that holds data permanently in the presence of power, whereas DRAM decays in seconds and must be periodically refreshed. Memory access via SRAM is much faster than DRAM, although DRAM circuits are much less expensive to construct.
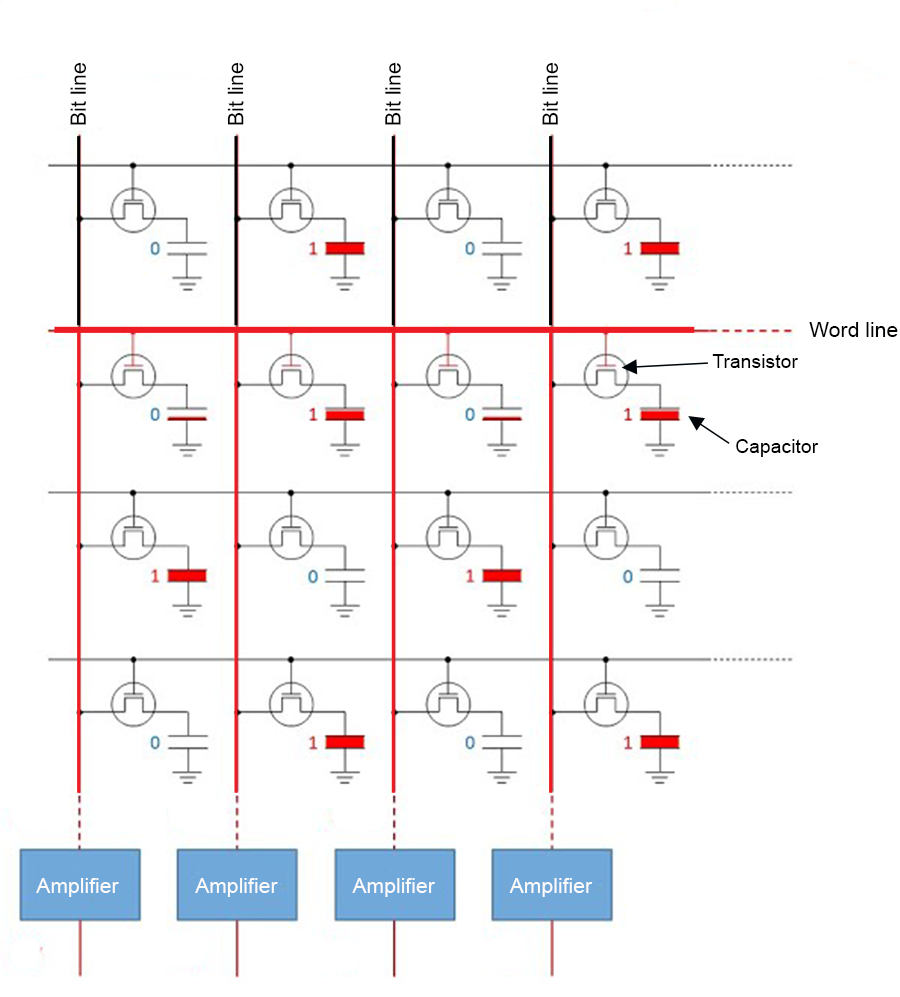
Figure 12.1: Sixteen DRAM memory cells each representing a bit of information for computational storage, reading, or writing. To read the binary word line 0101... in row two of the circuit, binary signals are sent down the bit lines to sense amplifiers.
Disk drives: including CD, DVD, hard disk (HDD), and solid state disk (SSD) are used for secondary memory. That is, memory that is not directly accessible from the CPU. Secondary memory can be accessed or retrieved even if the computer is off. Secondary memory is also non-volatile and thus can be used to store data and programs for extended periods. User files and software (like R) are generally stored on HDDs or SSDs. Flash memory, which uses modified metal–oxide–semiconductor field-effect transistors (MOSFETs), is typically used on USB and SSD devices to provide secondary memory that can be erased and reprogrammed. Flash memory can also be used in RAM applications.
Read-Only Memory (ROM): Stores the BIOS (see below) that runs when the computer is powered on (cold boot) or restarted (warm boot or reboot). ROM constitutes primary memory.
Basic Input Output System (BIOS): Basic boot (startup) and power management firmware (software that provides low level control for computer hardware). Newer motherboards use the so-called Unified Extensible Firmware Interface (UEFI) to address BIOS limitations, including restrictive 16 bit addresses.
Video card: Processes computer graphics.
12.2 Base-2 and Base-10
To understand computer processes, it is important to distinguish base-2 (binary) and base-10 (decimal) numerical systems. In both cases, the base refers to the number of unique digits. Thus, base-2 systems can have two unique digits, commonly \(0\) and \(1\), and the base-10 system has 10 unique digits: \(0,1,2,3,4,5,6,7,8,9\). The latter –more widely used system– probably arose because we have ten fingers for counting3. A radix (commonly a decimal symbol) is used to distinguish the integer part of a number from its fractional part (Fig 12.2). The radix convention is used by both base-2 and base-10 systems. For example, the decimal number \(4\frac{3}{4}\), has integer component \(4\) and fractional component \(\frac{3}{4}\), can be expressed as \(4.75\). The binary equivalent of \(4\frac{3}{4}\) is 100.110.
Traditionally, a base-10 number could only be expressed as a rational fraction whose denominator was a power of ten (Fig 12.2). However, the decimal system can be extended to any real number, by allowing a conceptual infinite sequence of digits following the radix (Wikipedia 2024b).
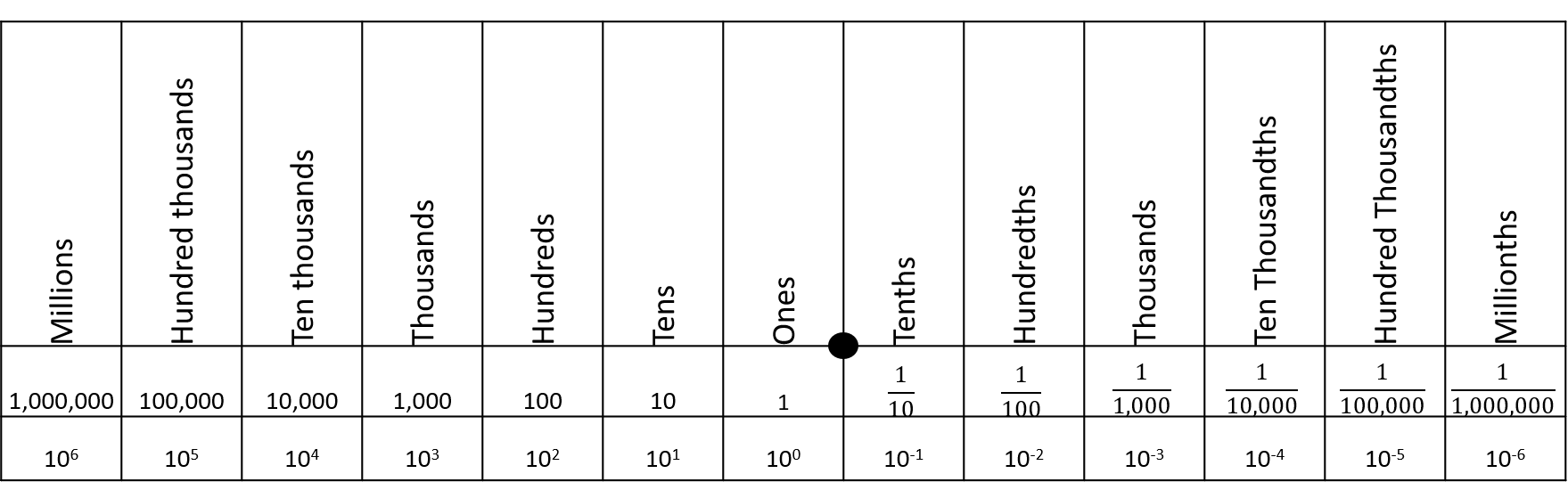
Figure 12.2: A decimal place value chart. A radix (decimal) is placed between the ones and thenths columns to distinguish decimal number components greater than one (to the left), and components less than one but greater than zero (to the right).
12.3 Bits and Bytes
Computers are designed around bits and bytes. A bit is a binary (base-2) unit of digital information. Specifically, a bit will represent a 0 or a 1. This convention occurs because computer systems typically use electronic circuits that exist in only one of two states, on or off. For instance, in DRAM memory cells (Fig 12.1) convert electrical low and high voltages into binary 0 and 1 responses, respectively, for the purpose of reading, writing, and storing data. Although bits are used by all software in all conventional computer operating systems, these mechanisms are easily revealed in R.
Bits are generally counted in units of bytes. For somewhat arbitrary historical reasons, a byte equals eight bits. Two major systems exist for counting bytes. The decimal method, the most common system, uses powers of 10, allowing implementation of SI prefixes (i.e., kilo = \(10^3 = 1000\), mega = \(10^6\) = \(1000^2\), giga = \(10^9\) = \(1000^3\), etc.) (Table 12.1). A computer hard drive with 1 gigabyte (1 billion bytes) of memory will have \(1 \times 10^9\) bytes = \(8 \times 10^9\) bits of memory. The binary system, used frequently by Windows to describe RAM, defines byte units in multiples of 1024.
| Decimal | Binary | ||
|---|---|---|---|
| Bytes | Name | Bytes | Name (IEC) |
| \(1000\) | kB (kilobyte) | \(1024\) | KiB (kibibyte) |
| \(1000^2\) | MB (megabyte) | \(1024^2\) | MiB (mebibyte) |
| \(1000^3\) | GB (gigabyte) | \(1024^3\) | GiB (gibibyte) |
| \(1000^4\) | TB (terabyte) | \(1024^4\) | TiB (tebibyte) |
| \(1000^5\) | PB (petabyte) | \(1024^5\) | PeB (pebibyte) |
With a single bit we can describe only \(2^1 = 2\) distinct digital objects. These will be an entity represented by a 0, and an entity represented by a 1. It follows that \(2^2 = 4\) distinct objects can be described with two bits, \(2^3 = 8\) entities can be described with three bits, and so on4.
12.4 Decimal to Binary
We count to ten in binary using: 0 = 0, 1 = 1, 10 = 2, 11 = 3, 100 = 4, 101 = 5, 110 = 6, 111 = 7, 1000 = 8, 1001 = 9, and 1010 = 10. Thus, we require four bits to count to ten. Note that the binary sequences for all positive integers greater than or equal to one, start with one.
12.4.1 Positive Integers
We can obtain the binary expression of the integer part of any decimal number by iteratively performing integer division by two, and cataloging each modulus. The iterations are stopped when a quotient of one is reached. The modulus sequence is read from right to left (backwards). If the whole number of interest is greater than one (i.e., the whole number is not 0 or 1) we place a one in front of the reversed sequence, because all binary sequences for numbers greater than or equal to one must start with one.
Example 12.1 \(\text{}\)
Consider the number 23:
\[ \begin{aligned} &\text{Modulus (remainder) }& 1& & 1& & 1& & 0&\\ &\text{Integer Quotient } & 23/2 = 11& & 11/2 = 5& & 5/2 = 2& & 2/2 = 1& \end{aligned} \]
The reversed sequence is 0111. We place a one in front to get the binary representation for 23: 10111. The function dec2bin() from asbio does the work for us:
[1] 10111\(\blacksquare\)
12.4.2 Positive Fractions
The fractional part of a decimal number can be converted to binary in a similar fashion.
- To identify the fractional expression as a non integer, start the binary sequence with
0.(a zero followed by a decimal symbol). - Double the fraction to be converted, and record a
1if the product is \(\ge 1\), and0otherwise. - For subsequent binary digits, multiply two by the fractional part of the previous multiplication. If the product is \(\ge 1\), record a
1. If not, record a0.
Example 12.2 \(\text{}\)
Consider the fraction \(\frac{1}{4}\). We have:
\[ \begin{aligned} &\text{Binary outcome}& 0 & & 1 && 0 && 0\\ &\text{Product}& 1/4 \times 2 = 1/2 < 1 & & 1/2 \times 2 = 1\ge 1 && 0 \times 2 = 0 < 1&& 0 \times 2 = 0 < 1 \end{aligned} \]
\(\blacksquare\)
We have a clear repeating sequence of zeroes, due to a product of two in the second step. This allows us to stop the growth of the binary expression. For fractions, the binary sequence is read conventionally, from left to right. Thus, the binary expression for \(\frac{1}{4}\) is 0.01 .
[1] 0.0112.5 Binary to Decimal
The addition of a binary digit (i.e., a bit) represents a doubling of information storage. For instance, as we increase from two bits to three bits, the number of describable integers increases from four (integers 0 to 3) to eight (integers 0 to 7). As a result we say that the rightmost digit in a set of binary digits represents \(2^0\), the next represents \(2^1\), then \(2^2\), and so on. This can be defined with an equation based on Horner’s method (Horner 1815) that allows conversion of binary to decimal numbers:
\[\begin{equation} \sum_{\kappa=\min(\kappa)}^{\max(\kappa)}\alpha\beta^\kappa \tag{12.1} \end{equation}\]
where \(\alpha\) is a quantity known as the significand, that contains bit (0, 1) outcomes. For the purpose of binary expressions, the modifying base, \(\beta\), is 2. The term \(\kappa\) is called (appropriately) the exponent.
The maximum and minimum values of \(\kappa\) are determined by counting the number of placeholder digits in the binary expression represented by the significand, with respect to a binary radix point (Fig 12.3). Note that counting starts with respect to 0 (the first digit to the left of the radix) for both positive (bits to the left of the radix) and negative (bits to the right of the radix) values of the exponent, \(\kappa\). The radix reference has prompted this method to be called floating point arithmetic.

Figure 12.3: Conceptualization of binary to decimal conversion, as given in Eq (12.1).
12.5.1 Positive Integers
For positive integers the entirety of the corresponding binomial expression will be to the left of the radix point (Fig 12.3). Thus, the minimum value of \(\kappa\) will be zero and the maximum value of \(\kappa\) will be the number of digits (bits) in the binary expression, minus one.
Equation (12.1) represents a dot product. That is, the equation is a sum of the element-wise multiplication of two vectors. For instance, to find the integers represented by a single binary bit, we multiply the binary digit value, 0 or 1, by the power of two it represents. Because the single bit signature would occur at the right-most address to the left of the radix, the value of exponent would be 0 (Fig 12.3). That is, \(\min(\kappa)\) = \(\max(\kappa)\) = 0 in Eq. (12.1).\
If the single bit equals 0 we have:
\[0 \times 2^0 = 0,\]
and if the single bit equals 1 we have:
\[1 \times 2^0 = 1.\]
Accordingly, to find the decimal version of a set of binary values, we take the sum of the products of the binary digits and their corresponding (decreasing) powers of base 2.
Example 12.3 \(\text{}\)
For example, the binary number 010101 equals:
\[\begin{aligned} (0 \times 2^5) + (1 \times 2^4) + (0 \times 2^3) + (1 \times 2^2) + (0 \times 2^1) + (1 \times 2^0) &= 0 + 16 + 0 + 4 + 0 +1 \\&= 21. \end{aligned} \]
The function bin2dec in asbio does the calculation for us.
[1] 21\(\blacksquare\)
12.5.2 Positive Fractions
For positive fractions, values of the \(\kappa\) exponent will decrease by minus one as bits increase by one (Fig 12.3). Thus, to obtain decimal fractions from binary fractions we multiply a bit’s binary value by decreasing negative powers of base two, starting at 0, and find the sum, as shown in Eq (12.1).
Example 12.4 \(\text{}\)
For example, the binary value 0.01 equals:
\[(0 \times 2^0) + (0 \times 2^{-1}) + (1 \times 2^{-2}) = 0.25\]
[1] 0.25\(\blacksquare\)
12.5.2.1 Terminality
Most decimal fractions will not have a clear terminal binary sequence. That is, a binary representation of a decimal fraction with a finite number of digits will not exist. This results in mere binary approximations of decimal numbers (Goldberg 1991). For instance, the 10 bit binary expression of \(\frac{1}{10}\) is
[1] 0.0001100110But translating this back to decimal we find:
[1] 0.0996Increasing the number of bits in the binary expression increases precision,
[1] 0.00011001100110but the decimal approximation remains imperfect.
[1] 0.10000000000000000555Note that the imperfect conversion above gives the actual result of the division \(\frac{1}{10}\) for all software on all current conventional computers (not just R)!
[1] 0.10000000000000000555It may seem surprising that rational fractions like \(\frac{1}{10}\) may have non-terminating binary expressions. Terminality, however, will only occur for a decimal fraction if a product of 2 results from the successive multiplication steps described in Section 12.4.2. This product does not occur for \(\frac{1}{10}\).
Lack of terminality for binary expressions prompts the need for quantifying imprecision in computers systems. This can be obtained from Eq (12.1). In particular, the exponent in Eq (12.1) determines minimum and maximum possible encoded numeric values, and the number of digits in the significand determines numeric precision. Indeed, by changing the base from 2 to 10, Eq (12.1) can be used to quantify the precision of binary and decimal numbers.
Example 12.5 \(\text{}\)
For instance, the decimal number \(1,245.42\) has the scientific notation: \(1.24542 \times 10^3\). The expression has a the precision of six digits, because under Eq (12.1) the significand has six digits. Note that applying these digits in Eq. (12.1) we have:
\[ \begin{aligned} 1 \times 10^3 & + & 2 \times 10^2 & + & 4 \times 10^1 & + & 5 \times 10^0 & + & 4 \times 10^{-1} & + &2 \times 10^{-2} & = \\ 1000 & + & 200 & + & 40 & + & 5 & + & 0.4 & + &0.02 & = 1245.42 \end{aligned} \]
\(\blacksquare\)
12.6 Double Precision
In most programs, on most workstations, the results of computations are stored as 32 bits (i.e., 4 bytes) or as 64 bits (8 bytes) of information. The 64 bit double precision format allows high precision representations of both positive and negative integers and their fractional components. Under this framework, one bit is allocated to the sign of the stored item, 53 bits are assigned to the significand, and 11 bits are given to the exponent (Fig 12.4).
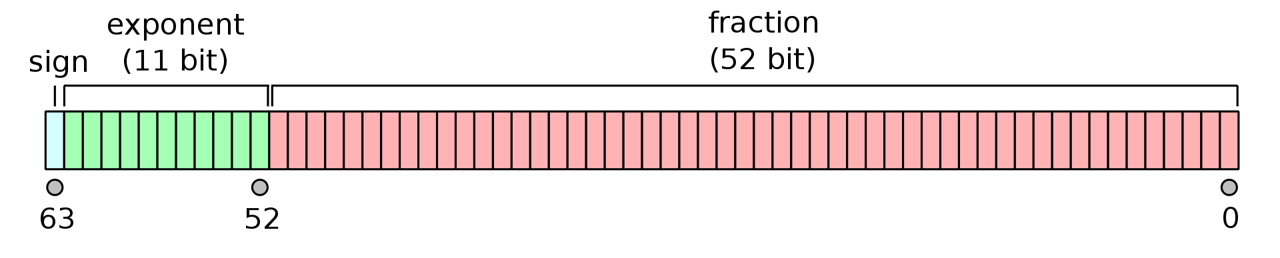
Figure 12.4: The IEEE 754 double-precision binary floating-point format Figure taken from (https://commons.wikimedia.org/w/index.php?curid=3595583).
This can be represented mathematically as a more complex form of Eq (12.1):
\[\begin{equation} (-1)^{\text{sign}}\left(1 + \sum_{i=1}^{52} b_{52-i} 2^{-i} \right)\times 2^{e-1023} \tag{12.2} \end{equation}\]
which gives the assumed numeric value for a 64-bit double-precision datum with exponent bias.\
Example 12.6 \(\text{}\)
The function bit64() below is taken from the Examples of the documentation for the base function numToBits(), which converts digital numbers to 64 bits. The function distinguishes:
- The single bit giving the sign of the number (
0= positive,1= negative). - The 11 bit exponent.
- A 52 bit significand (without the implicit leading
1).
bit64 <- function(x)
noquote(vapply(as.double(x),
function(x) {
b <- substr(as.character(rev(numToBits(x))), 2L, 2L)
paste0(c(b[1L], " ", b[2:12], " | ", b[13:64]), collapse = "")
}, "")
)Here is the double precision representation of \(\frac{1}{3}\)
[1] 0 01111111101 | 0101010101010101010101010101010101010101010101010101We see this follows the form of Eq (12.2). The exponent 01111111101 represents the decimal number 1021:
[1] 1021And one plus the dot product of the significand and base-2 raised to the sequence -1 to -52, multiplied by \(2^{1021 - 1023}\), is:
sigd <- strsplit("0101010101010101010101010101010101010101010101010101", NULL)
sigd <- as.numeric(unlist(sigd))
base2 <- 2^(-1:-52)
(1 + sum(sigd * base2)) * 2^-2[1] 0.3333That is, we have:
\[ \begin{aligned} value &= (-1)^{\text{sign}}\left(1 + \sum_{i=1}^{52} b_{52-i} 2^{-i} \right)\times 2^{e-1023}\\ &= -1^{0} \times (1 + 2^{-2} + 2^{-4} + \dots + 2^{-52}) \times 2^{1021-1023}\\ &\approx 1.33\bar{3} \times 2^{-2}\\ &\approx \frac{1}{3} \end{aligned} \]
\(\blacksquare\)
The 11 bit width of the double precision exponent allows the expression of numbers between \(10^{-308}\) and \(10^{308}\), with full 15–17 decimal digits precision. This is clearly demonstrated in R. Specifically, imprecision problems with non-terminal fractions become evident for decimal numbers with greater than 16 displayed digital digits.
[1] 0.333333333333333315Additionally, the current upper numerical limit in R (ver 4.3.2) is somewhere between:
[1] 1.8e+307and
[1] InfThe subnormal representation compromises precision, but allows allows fractional representations approaching \(5 \times 10^{-324}\). This approach is used by R, whose smallest represented fraction is between:
[1] 4.94065645841246544e-323and
[1] 0Binary fractional numbers are expressed with respect to a decimal, and the number of digits will (often) be dictated by the significand. Given 13 bits we have the following binary translations to decimal numbers: 1 = 1/1, 0.1 = 1/2, = 1/3, 0.01 = 1/4, 0.00110011 = 1/5, = 1/6, = 1/7, 0.001 = 1/8, = 1/9, = 1/10.
12.7 Binary Characters
Characters can also be expressed in binary. The American Standard Code for Information Interchange (ASCII) consists of 128 characters, and requires one byte = eight bits5. The newer eight bit Unicode Transformation Format (UTF-8) system –the most widely used Unicode system– can represent 1,112,064 valid code points, using between 1 to 4 bytes = 8 to 32 bits (Wikipedia 2024e). Specifically, from the perspective of the UTF-16 system, the UTF-8 system uses portions of seventeen planes^[In Unicode, a plane is a group of \(2^{16} = 65,536\) code points. There are 17 planes because UTF-16, can encode \(2^{20}\) code points (16 planes) as pairs of words, plus the so-called Basic Multilingual Plane (UTF-16 plane 0) as a single word.}, each consisting of sixteen bits (and, thus, \(2^{16} = 65,536\) code variants). This results in the quantity:
\[(17 \times 2^{16}) - 2^{11} = 1,112,064\]
The \(2^{11} = 2048\) subtraction acknowledges that there are 2048 technically-invalid Unicode surrogates (Wikipedia 2024d). The first 128 UTF-8 characters are the ASCII characters, allowing back-comparability with ASCII.
Example 12.7 \(\text{}\)
R uses the UTF-8 system of characters. We can observe the process of binary character assignment using the functions as.raw(), rawToChar(), and rawToBits().
Here is a list of the 128 ASCII characters.
[1] "\001" "\002" "\003" "\004" "\005" "\006" "\a" "\b" "\t" "\n"
[11] "\v" "\f" "\r" "\016" "\017" "\020" "\021" "\022" "\023" "\024"
[21] "\025" "\026" "\027" "\030" "\031" "\032" "\033" "\034" "\035" "\036"
[31] "\037" " " "!" "\"" "#" "$" "%" "&" "'" "("
[41] ")" "*" "+" "," "-" "." "/" "0" "1" "2"
[51] "3" "4" "5" "6" "7" "8" "9" ":" ";" "<"
[61] "=" ">" "?" "@" "A" "B" "C" "D" "E" "F"
[71] "G" "H" "I" "J" "K" "L" "M" "N" "O" "P"
[81] "Q" "R" "S" "T" "U" "V" "W" "X" "Y" "Z"
[91] "[" "\\" "]" "^" "_" "`" "a" "b" "c" "d"
[101] "e" "f" "g" "h" "i" "j" "k" "l" "m" "n"
[111] "o" "p" "q" "r" "s" "t" "u" "v" "w" "x"
[121] "y" "z" "{" "|" "}" "~" "\177" "\200" Note that the exclamation point is character number 33. Its 16 bit binary code is:
[1] 01 00 00 00 00 01 00 00From the output above, codes 1-31 and 127-128 are not printable characters. Thus, there are only 128 - 33 = 95 printable ASCII characters. Note that codes 7-13 are command characters. For instance, character 10, indicates ``make a new line’’ within a character string.
\(\blacksquare\)
12.8 Optimizing R
Because attention was given to computational efficiency in several earlier sections in this chapter, here I briefly consider several methods for optimizing R. In particular, I consider the use of R-interfaces, including scripting from command line OS shells to implement high performance computers (HPCs) and parallel computing.
Exercises
Define the following terms:
- Motherboard
- Central processing unit (CPU)
- Random access memory
- Primary memory
- Secondary memory
- Volatile memory
- Non-volatile memory
What is the level of trustworthy precision (in number of digits) for decimal fractional components in R (and all software that use 64 bit double precision)?
Obtain the five bit binary sequence for the number 21 by hand. Check your answer using
dec2bin().Find the decimal number corresponding to the five bit binary sequence
11111. Check your answer usingbin2dec().Find the 64 bit expression for the decimal number \(-2\) (minus 2) using the function
bit64(), as shown in this chapter. Back-transform this binary representation to the decimal number by hand using Eq. (12.2). Use R functions likestrsplit()unlist(), etc., to help.
References
A capacitor stores electrical energy by “accumulating electric charges on two closely spaced surfaces that are insulated from each other” (Wikipedia 2024a).↩︎
A transistor is a semiconductor device (a material with an intermediate electrical conductivity, e.g., silicon) that is used to amplify or switch electrical signals and power” (Wikipedia 2024c).↩︎
A base-20 system used by Pre-Columbian Mesoamerican cultures probably arose because we have twenty fingers and toes (Wikipedia 2024b).↩︎
For instance, images often contain eight bit (one byte) variables describing the colors red, green, and blue. Thus, the color red would be a number between 0 and 255 (i.e., red could have \(2^8 = 256\) distinct values). Given that the colors blue and green were also eight bit, there would be \(256^3 = 16,777,216\) color possibilities (combinations) for any pixel in an image.↩︎
Originally developed from telegraph code, ASCII has only 128 code points, of which only 95 are printable characters (Wikipedia 2023).↩︎