Chapter 2 Some Basics

“Learning to write programs stretches your mind, and helps you think better."

- Bill Gates, 1955-

2.1 First Steps

Upon opening R in Windows, two things will appear in the console of the R Graphical User Interface (R-GUI)¹. These are the license disclaimer (blue text at the top of the console) and the command line prompt, i.e., \(\boldsymbol{>}\) (Fig 2.1). The prompt indicates that R is ready for a command. All commands in R must begin at \(\boldsymbol{>}\).

The appearance of this simple interface will vary slightly among operating systems. In the Windows R-GUI, the command line prompt and user commands are colored red, and output, including errors and warnings, are colored blue. In Mac OS, the command line prompt will be purple, user inputs will be blue, and output will be black. In Unix/Linux, wherein R will generally run from a shell command line, absent of any menus, all three will be black².

We can exit R at any time by typing q() in the console, closing the GUI window (non-Linux only), or by selecting Exit from the pulldown File menu (non-Linux only).

Figure 2.1: An aged, but still recognizable R console: R version 2.15.1, “Roasted Marshmallows”, ca. 2012.

2.2 First Operations

As an introduction we can use R to evaluate a simple mathematical expression. Type 2 + 2 and press Enter.

2 + 2

[1] 4

The output term [1] means, “this is the first requested element.” In this case there is just one requested element, \(4\), the solution to \(2 + 2\). If the output elements cannot be held on a single console line, then R would begin the second line of output with the element number comprising the first element of the new line. For instance, the command rnorm(20) will take 20 pseudo-random samples (see footnote in Section 9.5.7) from a standard normal distribution (see Ch 3 in Aho (2014)). We have:

rnorm(20)

 [1]  1.0874948  0.1516419  0.4061965 -1.5421042 -0.7362779  0.9263209
 [7] -0.5693562  0.6988574  0.5190407 -0.2245550 -0.9101045 -0.7627200
[13] -0.4348216 -0.2454564 -0.8828227 -1.4213105 -0.7944881  0.4146818
[19] -0.4211308 -2.1329525

The reappearance of the command line prompt indicates that R is ready for another command. Multiple commands can be entered on a single line, separated by semicolons. Note, however, that this is considered poor programming style, as it may make your code more difficult to understand by a third party.

2 + 2; 3 + 2

[1] 4

[1] 5

R commands are generally insensitive to spaces. This allows the use of spaces to make code more legible. To my eyes, the command 2 + 2 is simply easier to read and debug than 2+2.

2.2.1 Use Your Scroll Keys

As with many other command line environments, the scroll keys (Fig 2.2) provide an important shortcut in R. Instead of editing a line of code by tediously mouse-searching for an earlier command to copy, paste and then modify, you can simply scroll back through your earlier work using the upper scroll key, i.e., \(\uparrow\) . Accordingly, scrolling down using \(\downarrow\) will allow you to move forward through earlier commands.

Figure 2.2: Typical scroll direction keys on a keyboard.

2.2.2 Note to Self: #

R will not recognize commands preceded by #. As a result this is a good way for us to leave messages to ourselves.

# Note at beginning of line
2 + 2

[1] 4

We can even place comments in the middle of an expression, as long the expression is finished on a new line.

2 + # Note in middle of line
+ 2

[1] 4

In the “best” code writing style it is recommended that one place a space after # before beginning a comment, and to insert two spaces following code before placing # in the middle of a line. This convention is followed above.

2.2.3 Unfinished Commands

R will be unable to move on to a new task when a command line is unfinished. For example, type

2 +

and press Enter. We note that the continuation prompt, +, is now where the command prompt should be. R is telling us the command is unfinished. We can get back to the command prompt by finishing the function, clicking Misc\(>\)Stop current computation or Misc\(>\)Stop all computations from the R-toolbar (non-Linux only), typing Ctrl + C (Linux), or by pressing the Esc key (all OS).

2.3 Expressions, Assignments and Objects

All entries in R are either expressions or assignments. If a command is an expression it will be evaluated, printed, and discarded. Examples include: 2 + 2. Conversely, an assignment evaluates an expression, and assigns a label to the output, but does not automatically print the result.

To convert an expression to an assignment we use the assignment operator, <-, which represents an arrow that points to the label of the expression. The assignment operator can go on either side of an expression.

Example 2.1 \(\text{}\)
If I type:

x <- 2 + 2

or

2 + 2 -> x

then an R-object is created named x that contains the result of the expression 2 + 2. In fact, the code: x <- 2 + 2 literally means: “x is \(2 + 2\).” To print the result (to see x), I simply type:

x

[1] 4

or

print(x)

[1] 4

\(\blacksquare\)

In Example 2.1 above we could have typed x = 2 + 2 with the same assignment results.

x = 2 + 2
x

[1] 4

However, for this document, I will continue to use the arrow operator, <-, for object assignments, and save the equals sign, =, for specifying arguments in functions (Ch 8).

Note that the R-console can quickly become cluttered and confusing. To remove clutter on the console (without actually getting rid of any of the objects created in a session) press Ctrl + L or, from the Edit pulldown menu, click on Clear console (non-Linux only).

2.3.1 Naming Objects

When assigning names to R-objects we should try to keep the names simple, and avoid names that already represent important definitions and functions. These include: TRUE, FALSE, NULL, NA, NaN, and Inf. In addition, we cannot have names:

• beginning with a numeric value,
• containing spaces, colons, and semicolons,
• containing mathematical operators (e.g., *, +, -, ^, /, =),
• containing important R metacharacters (e.g., @, #, ?, !, %, &, |).

However, even these “forbidden” names and characters can be used if one encloses them in backticks, also called accent grave characters. For example, the code, `?` <- 2 + 2 will create an object named `?`, containing the number 4.

Names should, if possible, be descriptive. Thus, for a object containing 20 random observations from a normal distribution, the name rN20 may be superior to the easily-typed, but anonymous name, x. Finally, we should remember that R is case sensitive. That is, each of the following \(2^4\) combinations will be recognized as distinct: name, Name, nAme, naMe, namE, NAme, nAMe, naME, NaMe, nAmE, NamE, naME, NAMe, nAME, NaME, NAmE, NAME.

2.3.2 Combining Data

To define a collection of numbers (or other data or objects) as a single entity one can use the important R function c, which means “combine”.

Example 2.2 \(\text{}\)
To define the numbers 23, 34, and 10 collectively as an object named x, I would type:

x <- c(23, 34, 10)

We could then do something like:

x + 7

[1] 30 41 17

Note that seven was added to each element in x.

\(\blacksquare\)

2.3.3 Object Classes

We can view everything created or loaded in R as an object³. Under the idiom of object oriented programming (OOP), an object may have attributes that allow it to be evaluated appropriately, and associated methods appropriate for those attributes (e.g., specific functions for plotting, printing, etc.)⁴.

I can list objects available in my R session using the function objects() or ls(). Currently, I only have x (which has been applied and modified several times) in my session (global environment):

# type:
objects()

[1] "x"

#or
ls()

[1] "x"

R objects will generally have a class, identifiable with the function class().

class(x)

[1] "numeric"

Objects in class numeric and several other common classes can be evaluated mathematically. Common R classes are shown in Table 2.1. We will create objects from all of these classes, and learn about their characteristics, over the next few chapters.

Table 2.1: Common R classes for some object x. The listed class would be printed if one created the assignment for x shown in the Example, and typed class(x)

Class	Example
logical	x <- TRUE
numeric	x <- 2 + 2
integer	x <- 1:3
character	x <- c("a","b","c")
factor	x <- factor("a","a","b")
complex	x <- 5i
expression	x <- expression(x * 4)
function	x <- function(y)y + 1
matrix	x <- matrix(nrow = 2, rnorm(4))
array	x <- array(rnorm(8), c(2, 2, 2))
data.frame	x <- data.frame(v1 = c(1,2), v2 = c("a","b"))
list	x <- list()

2.3.4 Object Base Types

All R objects will have so-called base types that define their underlying C language data structures⁵. There are currently 24 base types used by R (R Core Team 2024a), and it is unlikely that more will be developed in the near future (Wickham 2019). These entities are listed in Table 2.2. The meaning and usage of some of the base types may seem clear, for instance, integer and character, which are also class designations (Table 2.1). Other base types are be addressed in greater detail in later chapters, including list, logical, integer, and NULL (Ch 3), and closure, special, builtin, environment, pairlist, S4, promise, and symbol (Ch 8). Base types meant for C-internal processes, i.e., any, bytecode, promise, ..., weakref, externalptr, and char, are not easily accessible with interpreted R code (R Core Team 2024b).

Table 2.2: R base types. The listed base type would be printed if one created the assignment for x shown in the Example and typed typeof(x). The function mle, used to create the Example for base type S4, requires the package stats4.

Base type	Example	Application
NULL	x <- NULL	vectors
logical	x <- TRUE	vectors
integer	x <- 1L	vectors
complex	x <- 1i	vectors
double	x <- 1	vectors
list	x <- list()	vectors
character	x <- "a"	vectors
raw	x <- raw(2)	vectors
closure	x <- function(y)y + 1	closure functions
special	x <- `[`	special functions
builtin	x <- sum	builtin functions
expression	x <- expression(x * 4)	expressions
environment	x <- globalenv()	environments
symbol	x <- quote(a)	language components
language	x <- quote(a + 1)	language components
pairlist	x <- formals(mean)	language components
S4	x <- stats4::mle(function(x=1)x^2)	non-simple objects
any	No example	C-internal
bytecode	No example	C-internal
promise	No example	C-internal
...	No example	C-internal
weakref	No example	C-internal
externalptr	No example	C-internal
char	No example	C-internal

Base types of numeric objects define their storage mode, i.e., the way R caches them in its primary memory⁶. Base types can be identified using the function typeof().

typeof(x)

[1] "double"

We see that x has storage mode "double", meaning that its numeric values are stored using up to 53 bits, resulting in recognizable and distinguishable values between approximately \(5 \times 10^{-323}\) and \(2 \times 10^{307}\) (see Ch 12 for more information).

2.3.5 Object Attributes

Many R-objects will also have attributes (i.e., characteristics particular to the object or object class). Typing:

attributes(x)

NULL

indicates that x does not have additional attributes. However, using coercion (Section 3.3.2) we can define x to be an object of class matrix (a collection of data in a row and column format (see Section 3.1.2)).

attributes(as.matrix(x))

$dim
[1] 3 1

Now x has the attribute dim (i.e., dimension). Specifically, x is a three-celled matrix. It has three rows and one column.

Amazingly, classes and attributes allow R to simultaneously store and distinguish objects with the same name. For instance:

mean <- mean(c(1, 2, 3))
mean

[1] 2

mean(c(1, 2, 3))

[1] 2

In general, it is not advisable to name objects after frequently used functions. Nonetheless, the function mean(), which calculates the arithmetic mean of a collection of data, is distinguishable from the new user-created object mean, because these objects have different identifiable class characteristics. We can remove the user-created object mean, with the function rm(). This leaves behind only the function mean().

rm(mean)
mean

function (x, ...) 
UseMethod("mean")
<bytecode: 0x00000252fd2b2b00>
<environment: namespace:base>

The process of how these objects are distinguished by R is further elaborated in Section 8.8.

2.4 Getting Help

There is no single perfect source for information/documentation for all aspects of R. Detailed manuals from CRAN are available concerning the R language definition, basic operations, and package development. These resources, however, often assume a familiarity with Unix/Linux operating systems and computer science terminology. Thus, they may not be particularly helpful to biologists who are new to R.

2.4.1 help() and ?

A comprehensive help system is available for many R components including operators, and loaded package dataframes and functions. The system can be accessed via the question mark, ?, operator and the function help(). For instance, if I wanted to know more about the plot() function, I could type:

?plot

or

help(plot)

Documentation for packaged R functions (Section 3.5) must include an annotated description of function arguments, along with other pertinent information, and documentation for packaged datasets must include descriptions of dataset variables⁷. The quality of documentation will generally be excellent for functions from packages in the default R download (i.e., the R-distribution packages, see Section 3.5), but will vary from package to package otherwise. A list of arguments for a function, and their default values, can (often) be obtained using the function formals().

formals(plot)

$x


$y


$...

For help and documentation concerning programming metacharacters used in R (for instance @, #, ?, !, %, &, |), one would enclose the metacharacters with quotes. For example, to find out more information about the logical operator & I could type help("&") or ? "&". Placing two question marks in front of a topic will cause R to search for help files concerning with respect to all packages in a workstation. For instance, type:

??lm

or, alternatively

help.search(lm)

for a huge number of help files on linear model functions identified through fuzzy matching. Help for particular R-questions can often be found online using the search engine at http://search.r-project.org/. This link is provided in the Help pulldown menu in the R console (non-Linux only). Helpful online discussions can also be found at Stack Overflow, and Stats Exchange.

2.4.2 demo() and example()

The function demo() allows one access to coded examples that developers have worked out for a particular function or topic. For instance, type:

demo(graphics)

for a brief demonstration of R graphics. Typing

demo(persp)

will provide a demonstration of 3D perspective plots. And, typing:

demo(Hershey)

will provide a demonstration of available modifiable symbols from the Hershey family of fonts (see Ch 6 in Hershey (1967)). Finally, typing:

demo()

lists all of the demos available in the loaded libraries for a particular workstation. The function example() usually provides less involved demonstrations from the man package directories (short for user manual, see Ch 10) in an R package. For instance, type:

example(plotmath)

for a coded demonstration of mathematical graphics.

2.4.3 Vignettes

R packages often contain vignettes. These are short documents that generally describe the theory underlying algorithms and guidance on how to correctly use package functions. Vignettes can be accessed with the function vignette(). To view all vignettes for all installed packages (Section 3.5.1), type:

vignette(all = TRUE)

To view all vignettes available for loaded packages (see Section 3.5.2), type:

vignette(all = FALSE)

To view vignettes for the R contributed package asbio (following its installation), type:

vignette(package = "asbio")

To see the vignette simpson in package asbio, type:

vignette("simpson", package = "asbio")

The function browseVignettes() provides an HTML-browser that allows interactive vignette searches.

2.5 Options

To enhance an R session, we can adjust the appearance of the R-console and customize options that affect expression output. These include the characteristics of the graphics devices, the width of print output in the R-console, and the number of print lines and print digits. Changes to some of these parameters can be made by going to Edit\(>\)GUI Preferences in the R-toolbar. Many other parameters can be changed using the options() function. To see all alterable options one can type:

options()

The resulting list is extensive. To modify options, one would simply define the desired change within parentheses following a call to options. For instance, to see the default number of digits, I would type:

options("digits")

$digits
[1] 7

To change the default number of digits in output from 7 to 5 in the current session, I would type:

options(digits = 5)
# demonstration using pi
pi

[1] 3.1416

One can revert back to default options by restarting an R session.

2.5.1 Advanced Options

To store user-defined options and start up procedures, an.Rprofile file will exist in your R program etc directory. This location would be something like: \(\ldots\)R/R-version/etc. R will silently run commands in the .Rprofile file upon opening. Thus, by customizing the .Rprofile file one can “permanently” set session options, load installed packages, define your favorite package repository (Section 3.5), and even create aliases and defaults for frequently used functions.

The .Rprofile file located in the etc directory is the so-called .Rprofile.site file. Additional .Rprofile files can be placed in the working directory (see below). R will check for these and run them after running the .Rprofile.site file.

Example 2.3 \(\text{}\)
Here is the content of one of my current .Rprofile files.

options(repos = structure(c("http://ftp.osuosl.org/pub/cran/")))
.First <- function(){
library(asbio)
cat("\nWelcome to R Ken! ", date(), "\n")
}
.Last <- function(){
cat("\nGoodbye Ken", date(), "\n")
}

The command options(repos = structure(c("http://ftp.osuosl.org/pub/cran/"))) (Line 1) defines my preferred CRAN repository mirror site (Section 3.5). The function .First( ) (Lines 2-5) will be run at the start of the R session and .Last( ) (Lines 6-8) will be run at the end of the session. R functions will formally introduced in Ch 8. As we go through this book it will become clear that these lines of code force R to say hello, and to load the package asbio, and print the date/time (using the function date()) when it opens, and to say goodbye, and print the date/time when it closes (although the farewell will only be seen when running R from a shell interface, e.g., the Windows Command Prompt).

\(\blacksquare\)

One can create .Rprofile files, and many other types of R extension files using the function file.create(). For instance, the code:

file.create("defaults.Rprofile")

will place an empty, editable,.Rprofile file called defaults in the working directory.

2.6 The Working Directory

By default, the R working directory is set to be the home directory of the workstation. The command getwd() shows the current file path for the working directory.

getwd()

[1] "C:/Users/ahoken/Documents/Amalgam/Amalgam_Bookdown"

The working directory can be changed with the command setwd(filepath), where filepath is the location of the desired directory, or by using pulldown menus, i.e., File\(>\)Change dir (non-Linux only). Because R developed under Unix, we must specify directory hierarchies using forward slashes or by doubling backslashes.

Example 2.4 \(\text{}\)
To establish a working directory file path to the Windows directory: C:\Users\User\Documents, I would type:

setwd("C:/Users/User/Documents")

or

setwd("C:\\Users\\User\\Documents")

\(\blacksquare\)

2.7 Saving and Loading Your Work

As noted in Ch 1, an R session is allocated with a fixed amount of memory that is managed in an on-the-fly manner. An unfortunate consequence of this is that if R crashes, all unsaved information from the work session will be lost. Thus, session work should be saved often. Note that R will not give a warning if you are writing over session files from the R console. The old file will simply be replaced. Three general approaches for saving non-graphics data are possible. These are: 1) saving the history, 2) saving objects, and 3) saving R script. All three of these operations can be greatly facilitated by using an R integrated development environment (IDE) like RStudio (Section 2.9).

2.7.1 R History

To view the history (i.e., the commands that have been used in a session) one can use history(n) where n is the number of previous command lines one wishes to see⁸. For instance, to see the last three commands, one would type⁹:

history(3)

To save the session history in Windows one can use File\(>\)Save History or the function savehistory(). For instance, to save the session history to the working directory under the name history1, I could type:

savehistory(file = "history1.Rhistory")

We can view the code in this file from any text editor. To load the history from a previous session one can use File\(>\)Load History (non-Linux only) or the function loadhistory(). For instance, to load history1 I would type:

loadhistory(file = "history1.Rhistory")

To save the history at the end of (almost) every interactive Windows or Unix-alike R session, one can alter the .Rprofile file .Last function to include:

.Last <- function() if(interactive()) try(savehistory("~/.Rhistory"))

2.7.2 R Objects

To save all of the objects available in the current R-session one can use File\(>\)Save Workspace (non-Linux only), or simply type:

save.image()

This procedure saves session objects to the working directory as a nameless file using an .RData extension. The file will be opened, silently, with the inception of the next R- session, and cause objects used or created in the previous session to be available. Indeed, R will automatically execute all .RData files in the working directory for use in a session. Stored .RData files can also be loaded using File\(>\)Load Workspace (non-Linux only). One can also save .RData objects to a specific directory location and use a specific file name using: File\(>\)Save Workspace, or with flexible function save(). R data file formats, including .rda, and .RData, (extensions for R data files), and .R (the format for R scripts), can be read into R using the function load(). Users new to a command line environment will be reassured by typing:

load(file.choose())

The function file.choose() will allow one to browse interactively for files to load using dialog boxes. Detailed procedures for importing (reading) and exporting (saving) data with a row and column format, and an explicit delimiter (e.g. .csv files) are described in Ch 3.

2.7.3 R Scripts

To save an R script as an executable source file, it is best to use an integrated development environment (IDE) compatible with R. R contains its own IDE, the R-editor, which is useful for writing, editing, and saving scripts as .r extension files. To access the R-editor go to File\(>\)New script (non-Linux only) or type the shortcut Ctrl + F + N (Fig 2.3). Code written in the R IDE can be sent directly to the R-console by copying and pasting or by selecting code and using the shortcut Ctrl + R.

Figure 2.3: The R-editor providing code for a famous computational exercise.

Aside from the R-editor, a number of other IDEs outside of allow straightforward generation of R script files, and a direct link between text editors, that provide syntax highlighting for R code, and the R-console itself. These include RWinEdt (an R package plugin for WinEdt ), Tinn-R, a recursive acronym for Tinn is not Notepad, ESS (Emacs Speaks Statistics), Jupyter Notebook, a web-based IDE originally designed for Python, but useful for many languages, and particularly RStudio, which will be introduced later in this chapter¹⁰.

Saved R scripts can be called and executed using the function source(). To browse interactively for source code files, one can type:

source(file.choose())

or go to File\(>\)Source R code.

2.8 Basic Mathematics

A large number of mathematical operators and functions are available with a conventional download of R.

Elementary mathematical operators, common mathematical constants, trigonometric functions, derivative functions, integration approaches, and basic statistical functions are shown in shown in Tables 2.3 - 2.9.

2.8.1 Elementary Operations

Table 2.3: Elementary mathematical operators and functions in R. For all functions x represents a scalar or a numeric vector.

Operator	Operation	To find:	We type:
+	addition	\(2 + 2\)	2 + 2
-	subtraction	\(2 - 2\)	2 - 2
*	multiplication	\(2 \times 2\)	2 * 2
/	division	\(\frac{2}{3}\)	2/3
%%	modulo	remainder of \(\frac{5}{2}\)	5%%2
%/%	integer division	\(\frac{5}{2}\) without remainder	5%/%2
^	exponentiation	\(2^3\)	2^3
abs(x)	\(\mid x \mid\)	\(\mid -23.7 \mid\)	abs(-23.7)
round(x, digits = d)	round \(x\) to \(d\) digits	round \(-23.71\) to 1 digit	round(-23.71, 1)
ceiling(x)	round \(x\) up to closest whole num.	ceiling(2.3)	ceiling(2.3)
floor(x)	round \(x\) down to closest whole num.	floor(2.3)	floor(2.3)
sqrt(x)	\(\sqrt{x}\)	\(\sqrt{2}\)	sqrt(2)
log(x)	\(\log_e{x}\)	\(\log_e{5}\)	log(5)
log(x, base = b)	\(\log_b{x}\)	\(\log_{10}{5}\)	log(5, base = 10)
factorial(x)	\(x!\)	\(5!\)	factorial(5)
gamma(x)	\(\Gamma(x)\)	\(\Gamma(3.2)\)	gamma(3.2)
choose(n,x)	\(\binom{n}{x}\)	\(\binom{5}{2}\)	choose(5,2)
sum(x)	\(\sum_{i=1}^{n}x_i\)	sum of x	sum(x)
cumsum(x)	cumulative sum	cum. sum of x	cumsum(x)
prod(x)	\(\prod_{i=1}^{n}x_i\)	product of x	prod(x)
cumprod(x)	cumulative product	cum. prod. of x	cumprod(x)

2.8.2 Associativity and Precedence

Note that the operation:

2 + 6 * 5

[1] 32

is equivalent to \(2 + (6 \cdot 5) = 32\). This is because the * operator gets higher priority (precedence) than +. Evaluation precedence can be modified with parentheses:

(2 + 6) * 5

[1] 40

In the absence of operator precedence, mathematical operations in R are (generally) read from left to right (that is, their associativity is from left to right) (Table 2.4). This corresponds to the conventional order of operations in mathematics. For instance:

2 + 2^(2 + 1)

[1] 10

Table 2.4: Precedence and associativity of mathematical operators. Operators are listed from highest to lowest precendece in operations.

Precedent	Operator	Description	Associativity
1	^	exponent	right to left
2	%%	modulo	left to right
3	* /	multiplication, division	left to right
4	+ -	addition, subtraction	left to right

2.8.3 Function Arguments

R functions generally require a user to specify arguments (in parentheses) following the function name. For instance, sqrt() and factorial() each require one argument, a call to data itself. Thus, to solve \(1/\sqrt{22!}\), I could type:

1/sqrt(factorial(22))

[1] 2.9827e-11

To solve \(\Gamma \left( \sqrt[3]{23\pi} \right)\), I could type:

gamma((23 * pi)^(1/3))

[1] 7.411

By default the function log() computes natural logarithms, i.e.,

log(exp(1))

[1] 1

The log() function can also compute logarithms to a particular base by specifying the base in an optional second argument called base. For instance, to solve the operation: \(\log_{10}3 + \log_{3}5\), one could type:

log(3, 10) + log(5, 3)

[1] 1.9421

Arguments can be specified by the order that they occur in the list of arguments in the function code, or by calling the argument by name. In the code above I know that the first argument in log() is a call to data, and the second argument defines the base. I may not, however, remember the argument order in a function, or may wish to only change certain arguments from a large allotment. In this case it is better to specify an argument by calling its name and defining its value with an equals sign.

log(x = 3, base = 10) + log(x = 5, base = 3)

[1] 1.9421

2.8.4 Constants

R allows easy access to most conventional constants (Table 2.5).

Table 2.5: Conventional constants in R.

Operator	Operation	To find:	We type:
-Inf	\(-\infty\)	\(-\infty\)	-Inf
Inf	\(\infty\)	\(\infty\)	Inf
pi	\(\pi = 3.141593 \dots\)	\(\pi\)	pi
exp(1)	\(e = 2.718282 \dots\)	\(e\)	exp(1)
exp(x)	\(e^x\)	\(e^3\)	exp(3)

2.8.5 Trigonometry

R assumes that the inputs for trigonometric functions are in radians. Of course degrees can be obtained from radians using \(Degrees = Radians \times 180/\pi\), or conversely \(Radians = Degrees \times \pi /180\) (Table 2.6).

Table 2.6: Trigonometric functions in R. For all functions x represents a scalar or a numeric vector.

Operator	Operation	To find:	We type:
cos(x)	\(\text{cos}(x)\)	\(\text{cos}(3 \text{ rad.})\)	cos(3)
sin(x)	\(\text{sin}(x)\)	\(\text{sin}(45^{\circ})\)	sin(45 * pi/180)
tan(x)	\(\text{tan}(x)\)	\(\text{tan}(3 \text{ rad.})\)	tan(3)
acos(x)	\(\text{acos}(x)\)	\(\text{acos}(45^{\circ})\)	acos(45 * pi/180)
asin(x)	\(\text{asin}(x)\)	\(\text{asin}(3 \text{ rad.})\)	asin(3)
atan(x)	\(\text{atan}(x)\)	\(\text{atan}(45^{\circ})\)	atan(45 * pi/180)

2.8.6 Derivatives

The function D() finds symbolic and numerical derivatives of simple expressions. It requires two arguments, a mathematical function specified as an expression (i.e., an object of class and base type expression, created using the function expression(), that can be evaluated with the function eval()), and the denominator in the difference quotient. Here is an example of how functions expression and eval() are used:

eval(expression(2 + 2))

[1] 4

Of course we wouldn’t bother to use expression() and eval() in such simple applications. Table 2.7 contains specific examples using D().

Table 2.7: Evaluation of derivatives in R.

To find:	We type:
\(\frac{d}{dx}5x\)	D(expression(5 * x), "x")
\(\frac{d^2}{dx^2} 5x^2\)	D(D(expression(5 * x^2), "x"), "x")
\(\frac{\partial}{\partial x} 5xy + y\)	D(expression(5 * x * y + y), "x")

2.8.7 Integration

The function integrate solves definite integrals. It requires three arguments. The first is an R function defining the integrand. The second and third are the lower and upper bounds of integration.

Example 2.5 \(\text{}\)
To solve: \[\int^4_2 3x^2dx\] we could type:

f <- function(x){3 * x^2}
integrate(f, 2, 4)

56 with absolute error < 6.2e-13

R functions are explicitly addressed in Ch 8. ### Statistics R, of course, contains a huge number of statistical functions. These will generally require sample data for summarization. Data can be brought into R from spreadsheet files or other data storage files (we will learn how to do this shortly). As we have learned, data can also be assembled in R. For instance,

x <- c(1, 2, 3)

Statistical estimators can be separated into point estimators, which estimate an underlying parameter that has a single true value (from a Frequentist viewpoint), and intervallic estimators, which estimate the bounds of an interval that is expected, preceding sampling, to contain a parameter at some probability (Aho 2014). Point estimators can be further classified as estimators of location, scale, shape, and order statistics (Table 2.8). Measures of location estimate the typical or central value from a sample. Examples include the arithmetic mean and the sample median. Measures of scale quantify data variability or dispersion. Examples include the sample standard deviation and the sample interquartile range (IQR). Shape estimators describe the shape (i.e., symmetry and peakedness) of a data distribution. Examples include the sample skewness and sample kurtosis. Finally, the \(k\)th order statistic of a sample is equal to its \(k\)th-smallest value. Examples include the data minimum, the data maximum, and other quantiles (including the median). Intervallic estimators include confidence intervals (Table 2.9). A huge number of other statistical estimating, modelling, and hypothesis testing algorithms are also available for the R environment. For guidance, see Venables and Ripley (2002), Aho (2014), and Fox and Weisberg (2019), among others.

Table 2.8: Simple point estimators in R. The term x represents a numeric data vector, and y represents a numeric data vector whose elements are paired with those in x. The cipher asbio:: indicates that the function is located in the package asbio.

Function	Acronym	Description	Estimator type
mean(x)	\(\bar{x}\)	arithmetic mean of \(x\)	location
mean(x, trim = t)		trimmed mean of \(x\) for \(0 \leq t \leq 1\).	location
asbio::G.mean(x)	\(GM\)	geometric mean of \(x\)	location
asbio::H.mean(x)	\(HM\)	harmonic mean of \(x\)	location
median(x)	\(\tilde{x}\)	median of \(x\)	location order statistic
asbio::Mode(x)	\(mode(x)\)	mode of \(x\)	location
sd(x)	\(s\)	standard deviation of \(x\)	scale
var(x)	\(s^2\)	variance of \(x\)	scale
cov(x, y)	\(cov(x,y)\)	covariance of \(x\) and \(y\)	scale
cor(x, y)	\(r_{x,y}\)	Pearson correlation of \(x\) and \(y\)	scale
IQR(x)	\(IQR\)	interquartile range of \(x\)	scale order statistic
mad(x)	\(MAD\)	median absolute deviation of \(x\)	scale
asbio::skew(x)	\(g_1\)	skew of \(x\)	shape
asbio::kurt(x)	\(g_2\)	kurtosis of \(x\)	shape
min(x)	\(min(x)\)	min of \(x\)	order statistic
max(x)	\(max(x)\)	max of \(x\)	order statistic
quantile(x, prob = p)	\(\hat{F}^{-1}(p)\)	quantile of \(x\) at lower-tailed probability \(p\)	order statistic

Table 2.9: Some intervallic estimators in R. The term x represents a numeric vector. The cipher asbio:: indicates that the function is located in the package asbio

Function	Description
asbio::ci.mu.z(x, conf, sigma)	Conf. int. for \(\mu\) at level conf. True SD = sigma.
asbio::ci.mu.t(x, conf)	Conf. int. for \(\mu\) at level conf. \(\sigma\) unknown.
asbio::ci.median(x, conf)	Conf. int. for true median at level conf.

2.9 RStudio

RStudio is an open source IDE for R (Fig 2.4). RStudio greatly facilitates writing R code, saving and examining R objects and history, and many other processes. These include, but are not limited to, documenting session workflows, writing R package documentation, calling and receiving code from other languages, and even developing web-based graphical user interfaces. RStudio can currently be downloaded at (https://posit.co/products/open-source/rstudio/). Like R itself, RStudio can be used with Windows, Mac, and Unix/Linux operating systems, RStudio has both freeware and commercial versions¹¹. We will use the former here.

Figure 2.4: The RStudio logo.

RStudio is generally implemented using a four pane workspace (Fig 2.5). These are: 1) the code editor, 2) R-console, 3) Environment and histories, 4) Plots and other miscellany.

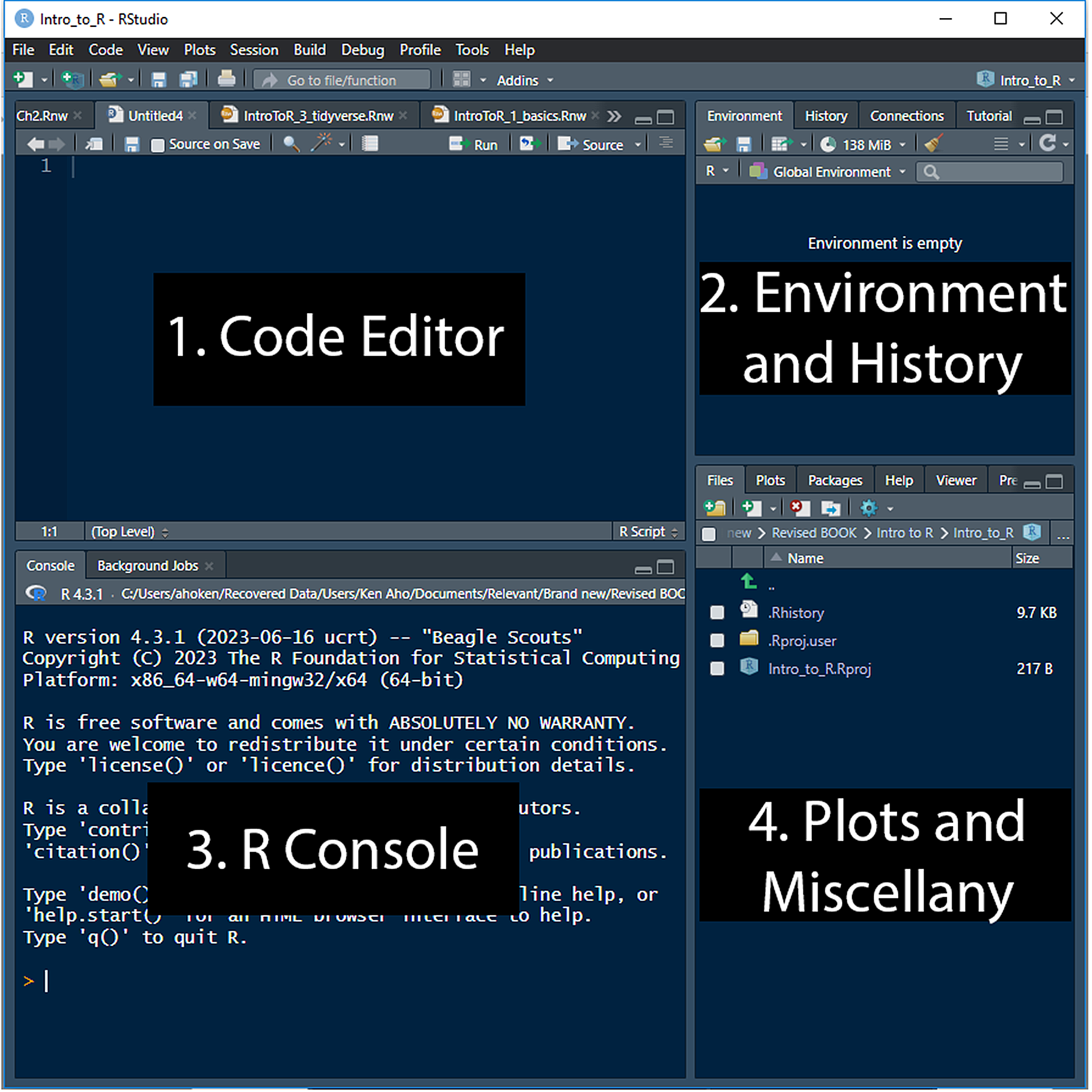
Figure 2.5: Interfaces for RStudio 2023.06.2 Build 561.

• The RStudio code editor panel (Fig 2.5, Panel 1) allows you to create R scripts and scripts for other languages that can be called to and from R. The code panel can also be used to create and edit session documentation files (see Section 2.9.2 below) and other important R file types. A new R script can be created for editing within the code editor by going to File\(>\)New\(>\)R Script. Commands from an R script can be sent to the R console using the shortcut Ctrl + Enter (Windows and Linux) or Cmd + Enter (Mac).

• The R console panel (Fig 2.5, Panel 2) by default, is identical in functionality to the R console of the most recent version of R on your workstation (assuming that all of the paths and environments are set up correctly on your computer). Thus, the console panel can be used directly for typing and executing R code, or for receiving commands from the code editor (Panel 1).

• The environments and history panel (Fig 2.5, Panel 3) can be used to: 1) show a list of R objects available in your R session (the Environment tab), or 2) show, search, and select from the history of all previous commands (History tab). This panel also provides an interface for point and click import of data files including .csv, .xls, and many other file formats (Import Dataset pulldown within the Environment tab).

• The plots and files panel (Fig 2.5, Panel 4) can be used to show: 1) files in the working directory, 2) a scrollable history of plots and image files, and 3) a list of available packages (via the Packages tab), with facilities for updating and installing packages. If a package is in the GUI list, then the package is currently loaded. Packages and their installation, updating, and loading are formally introduced in Section 3.5. The panel’s Files pulldown tab allows straightforward establishment of working directories (although this can still be done at the command line using setwd()) (Fig 2.7). The panel’s Help tap opens automatically when uses ? or help for particular R topics (Section 2.4).

CAUTION!

Be very careful when managing files in the plots and files panel, as you can permanently delete files without (currently) the possibility of recovery from a Recycling Bin.

2.9.1 RStudio Project

An RStudio project can be be created via the File pulldown menu (Fig 2.7). A project allows all related files (data, figures, summaries, etc.) to be easily organized together by setting the working directory to be the location of the project .Rproj file.

2.9.2 Workflow Documentation

We can document workflow and simultaneously run/test R session code by either:

1. creating an R Markdown .rmd file that can be compiled to make a .html, .pdf, or MS Word .doc document¹², or
2. using Sweave, an approach that implements the LaTeX (pronounced lay-tek) document preparation system.

2.9.2.1 R Markdown

The R Markdown document processing workflow in RStudio is shown Fig 2.6. These steps are highly modifiable, but can also be run in a more or less automated manner, requiring little understanding of underlying processes.

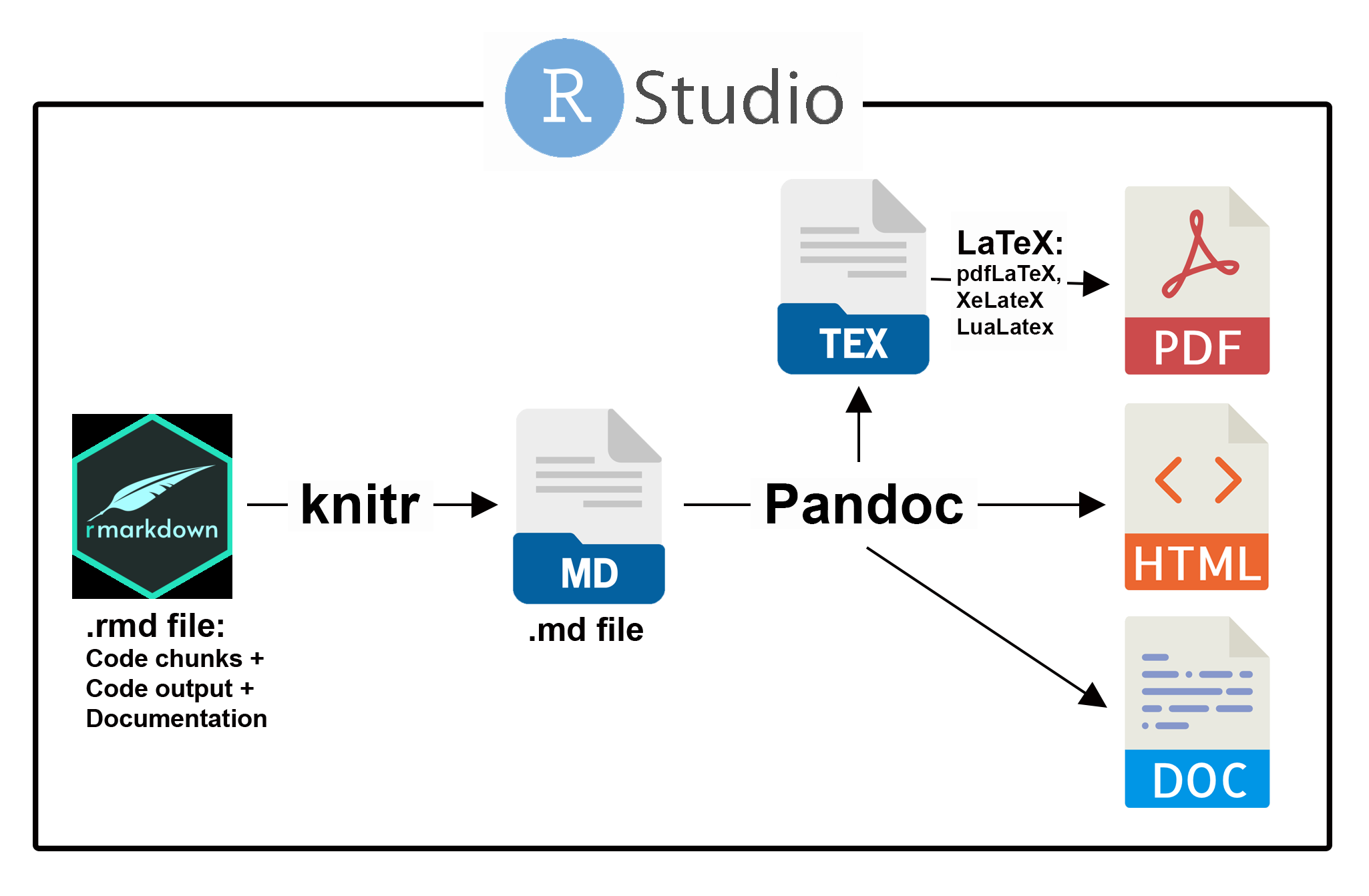
Figure 2.6: The process of document creation in R Markdown. Functions in the package rmarkdown control conversion of .rmd files to Markdown .md files, using utilities in the package knitr. Pandoc first creates a .tex file when rendering LaTeX PDF documents.

Use of R Markdown and .rmd files requires the package rmarkdown (Allaire et al. 2024), which comes pre-installed in RStudio.

As an initial step, all underlying .rmd files must include a brief YAML¹³ header (see below) containing document metadata. The remainder of the .rmd document will contain text written in Markdown syntax, and code chunks. The knit() function from package knitr Xie (2015), also installed with RStudio, executes all evaluable code within chunks, and formats the code and output for processing within Pandoc, a program for converting markup files from one language to another¹⁴. Pandoc uses the YAML header to guide this conversion. As an example, if one has requested HTML output, the simple Markdown text: This is a script will be converted to the HTML formatted: <p>This is a script</p>. One can also write HTML script directly into an .rmd document (see Section 11.5). If the desired output is PDF, Pandoc will convert the .md file into an intermediate .tex file. This file is then processed by LaTeX, an open source, high-quality scientific typesetting system¹⁵. LaTeX compiles the .tex file into a .pdf file. In this process, the tinytex package (Xie 2024), which installs the stripped-down LaTeX distribution TinyTex, can be used.

A brief introduction to R Markdown can be found at: http://rmarkdown.rstudio.com. A thorough description of R Markdown is given in Xie, Allaire, and Grolemund (2018) and Xie, Dervieux, and Riederer (2020). The latter text is currently available as an online resource.

Creating an R Markdown document is simple in RStudio. We first open an empty .rmd document by navigating to File \(>\) New File \(>\)R Markdown (Fig 2.7).

Figure 2.7: Part of the RStudio File pulldown menu.

You will delivered to the GUI shown in Fig 2.8. Note that by default Markdown compilation generates an HTML document.

Figure 2.8: RStudio GUI for creating an R Markdown document.

The GUI opens a R Markdown (.rmd) skeleton document with a tentative YAML header.

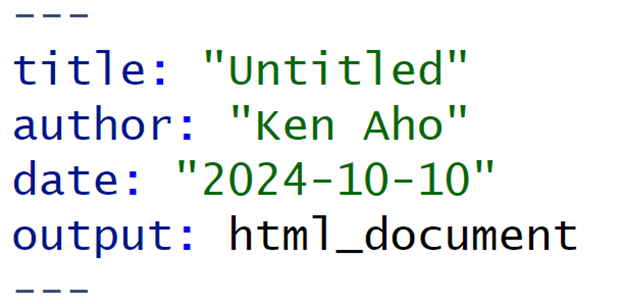
Figure 2.9: YAML header to an R Markdown (.rmd) skeleton document.

The HTML output can be changed to one of:

output: pdf_document

or

output: word_document

depending on the style of document one desires.

The knitr package facilitates report building in both HTML and LaTeX formats, within the framework of rmarkdown (Fig 2.6). Under knitr, R Markdown lines beginning ```{r } and ending ``` delimit an R code “chunk” to be potentially run in the R environment. The chunk header, ```{r }, can contain additional options. For a complete list of chunk options, run

str(knitr::opts_chunk$get())

Code chunks can be generated by going to Code\(>\)Insert Chunk or by using the RStudio shortcut Ctrl + Alt + I (Windows and Linux) or Cmd + Alt + I (Mac). R code can also be invoked inline in a R Markdown document using the format:

`r some code`

For instance, I could seamlessly place three random numbers generated from a the continuous uniform distribution, \(f(x) = UNIF(0,1)\), inline into text using:

`r runif(3)`

Here I run an iteration using “hidden” inline R code: 0.41526, 0.29302, 0.45674.

In Markdown, pound signs (e.g., #, ##, ###) can be used as (increasingly nested) hierarchical section delimiters.

Inline equations for both Markdown and Sweave (discussed below) can be specified under the LaTeX system, which uses dollar signs, $, to delimit equations. For instance, to obtain the inline equation: \(P(\theta|y) = \frac{P(y|\theta)P(\theta)}{P(y)}\), i.e., Bayes theorem, I could type the LaTeX script:

$(\theta|y) = \frac{P(y|\theta)P(\theta)}{P(y)}$

A cheatsheet for LaTeX equation writing can be found here.

The R Markdown (.rmd) skeleton file has example documentation text, interspersed with example R code in chunks. These been have been modified below to create a simple summary document for the dataset Loblolly from the package datasets (Fig 2.10), which describes growth characteristics of loblolly pine trees (Pinus taeda).

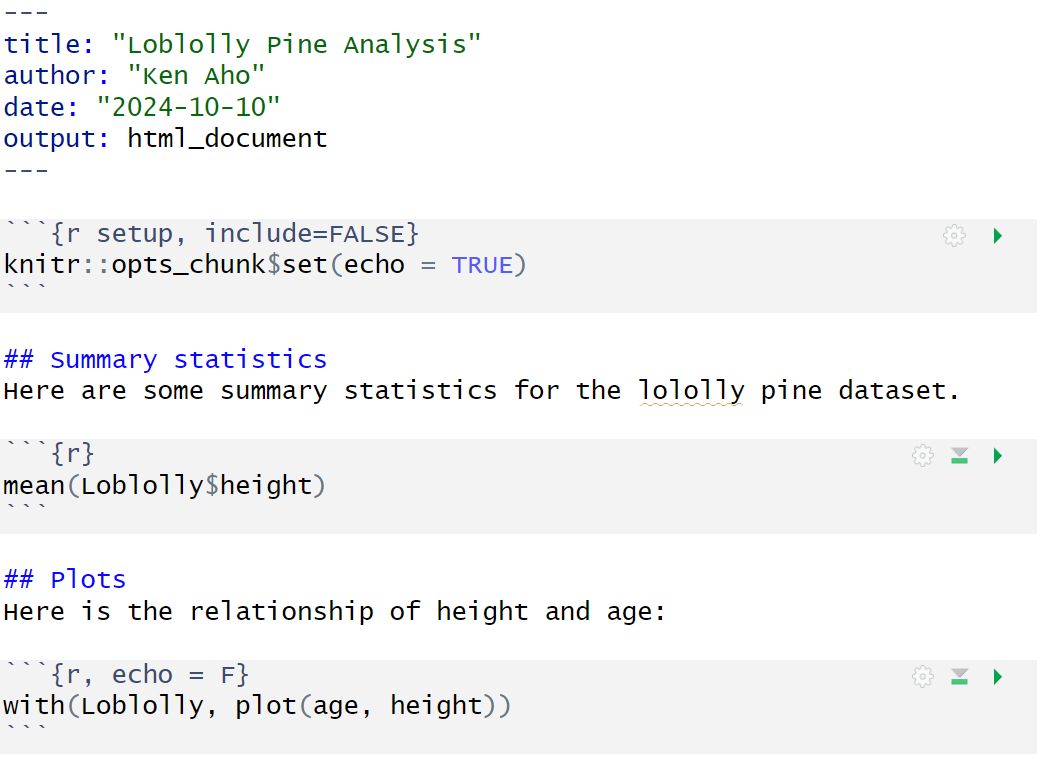
Figure 2.10: An R Markdown (.rmd) file with documentation text and interspersed R code in chunks.

Note the use of echo = FALSE in the final chunk to suppress printing of R code. A snapshot of the knitted HTML is shown in Fig 2.11.

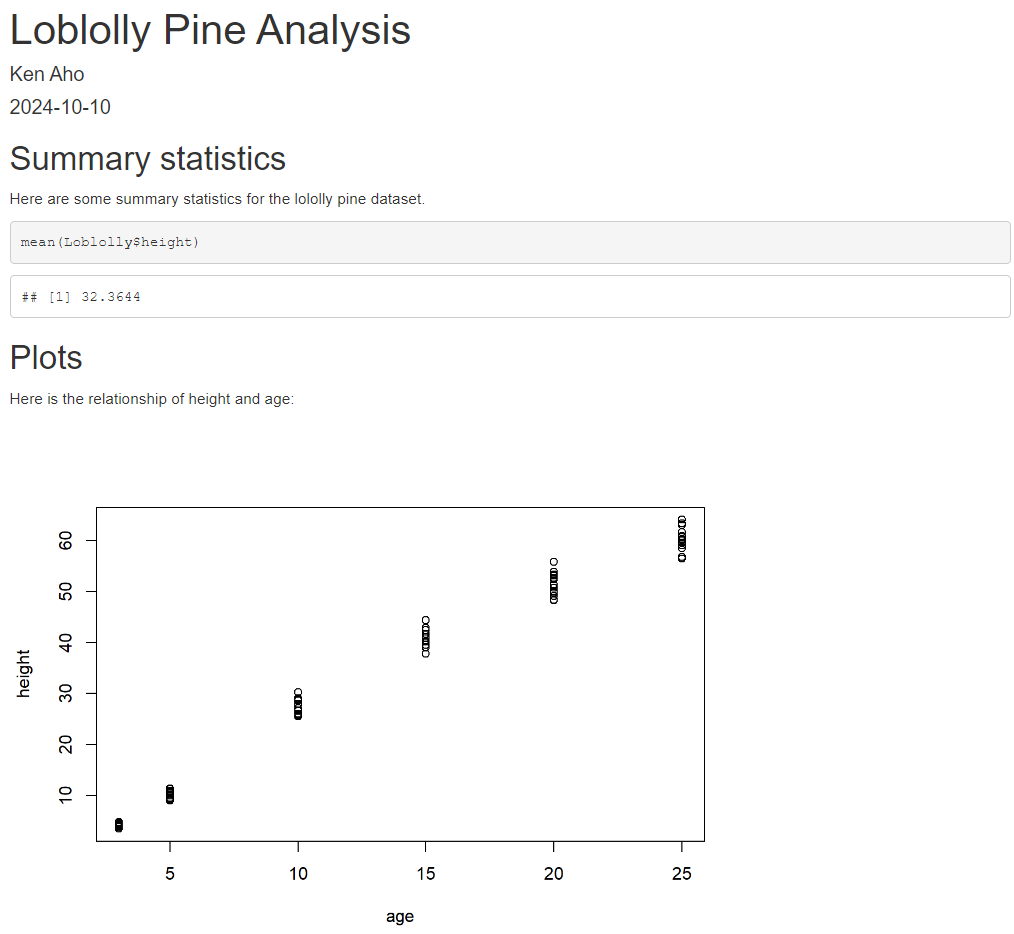
Figure 2.11: An HTML document knit from Markdown code in the previous figure. Note that code is displayed (by default) as well as executed.

I generally use the function knitr::kable() to create R Markdown \(\rightarrow\) Pandoc \(\rightarrow\) HTML tables because it is relatively simple to use. The code below was used to create Table 2.10.

knitr::kable(head(Loblolly))

Table 2.10: Loblolly pine data

	height	age	Seed
1	4.51	3	301
15	10.89	5	301
29	28.72	10	301
43	41.74	15	301
57	52.70	20	301
71	60.92	25	301

I often use functions in the package xtable to build R Markdown \(\rightarrow\) Pandoc \(\rightarrow\) LaTeX \(\rightarrow\) PDF tables. Under this approach, one could create Table 2.10 using:

print(xtable::xtable(head(Loblolly)))

This method would also require that one use the command results = 'asis' in the chunk options. One can even call for different table approaches on the fly. For instance, I could use the command eval = knitr::is_html_output()), in the options of a Markdown chunk when using table code that optimizes HTML formatting, and use eval = knitr::is_latex_output()) to create a table that optimizes LaTeX formatting. Aside from knitr::kable() and xtable, there are many other R functions and packages that can be used to create R Markdown tables, particularly for HTML output. These include:

• The kableExtra (Zhu et al. 2022) package extends knitr::kable() by including styles for fonts, features for specific rows, columns, and cells, and straightforward merging and grouping of rows and/or columns. Most kableExtra features extend to both HTML and PDF formats.
• DT (Xie, Cheng, and Tan 2024), a wrapper for HTML tables that uses the JavaScript (see Section 11.3) library DataTables. Among other features, DT allows straightforward implementation in interactive Shiny apps (Section 11.5).
• Like DT, the reactable package (Lin 2023) creates flexible, interactive HTML embedded tables. As with DT, reactable tables add complications when those interactives are considered as conventional tables in R markdown, with captions and referable labels.

Xie, Dervieux, and Riederer (2020) discuss several other alternatives.

Below I use the function reactable() from the reactable package to create a table with sortable columns and scrollable rows (Table 2.11).

# install.packages("reactable")
library(reactable)
reactable(Loblolly, pagination = FALSE, highlight = TRUE, height = 250)

Table 2.11: Interactive table for the Loblolly dataframe generated using reactable::reactable().

2.9.2.1.1 Bookdown

A large number of useful auxiliary features are available for R Markdown, through the R package bookdown (Xie (2016), Xie (2023)). These include an extended capacity for figure, table, and section numbering and referencing. To use bookdown we must modify the output: designation in the YAML header to be one of the following:

output: bookdown::html_document2

or

output: bookdown::pdf_document2

or

output: bookdown::word_document2

depending on the desired document format.

Numbering R-generated plots and tables in R Markdown or Bookdown requires specification of a chunk label after the language reference r in the chunk generating the plot. In the chunk below I use the label lobplot. Note that a space is included after r. Captions are specified in the chunk header using the chunk option fig.cap or tab.cap for figures and tables, respectively. For instance,

```{r lobplot, echo=FALSE, fig.cap= "Loblolly pine height versus age."}

Cross-references within the text can be made using the syntax \@ref(type:label), where label is the chunk label and type is the environment being referenced (e.g., fig, tab, or eq). For the current example, we might want to type something like: “see Figure \@ ref(fig:lobplot)”. in some non-chunk component of the Markdown document.

Specification of output: bookdown::html_document2, or one of the other two bookdown document options, will result in automated numbering of sections. To turn this numbering off, one could modify the YAML output to be:

output:
  bookdown::html_document2:
    number_sections: false

The code indents shown above are important because YAML, like the language Python, uses significant indentation. To omit numbering for certain sections, one would retain the bookdown output, and add {-} after the unnumbered section heading, e.g.,

# This section is unnumbered {-}

For additional details see: ?bookdown::html_document2 and Xie (2016).

2.9.2.2 Sweave

Under the Sweave documentation approach, high quality .pdf documents are generated from LaTeX .tex files, which in turn are created from Sweave .rnw files. This can also be facilitated with RStudio. A skeleton .rnw document can be generated by going to File\(>\)New File\(>\)R Sweave¹⁶. In Fig 2.12 I create an .rnw file with the text and analyses used in the Markdown example above (Figs 2.10-2.11). We note that instead of the Markdown YAML header, we now have lines in the preamble defining the type of desired document (e.g., article) and the LaTeX packages needed for document compilation (e.g, amsmath). Note that R code chunks are now initiated by <<>>=, which serves as a chunk header and can contain options, and closed with @. Non-code text, including figure and table captions and cross-referencing should follow LaTeX guidelines.

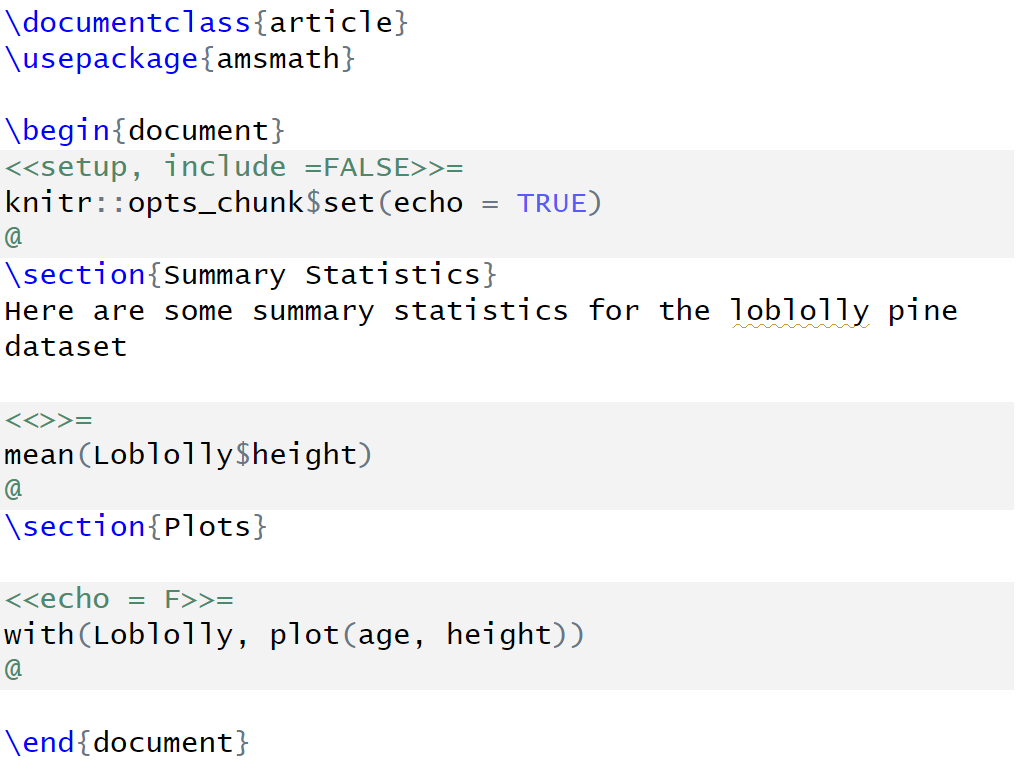
Figure 2.12: A Sweave (.rnw) file with documentation text and interspersed code in chunks.

Fig 2.13 shows a snapshot of the .pdf result, following Sweave/LaTeX compilation.

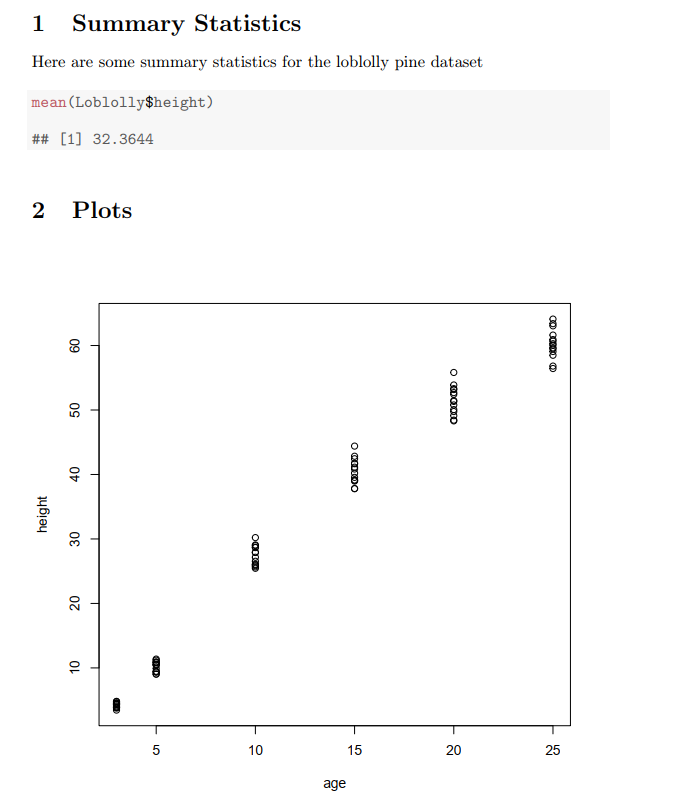
Figure 2.13: A .pdf document resulting from compilation of Sweave code in the previous figure.

2.9.2.3 Purl

R code can be extracted from an .rmd or or an .rnw file using the function knitr::purl(). For instance, assume that the R Markdown loblolly pine summary shown in Fig 2.10 is saved in the working directory under the name lob.rmd. Code from the file will be extracted to a script file called lob.R, located in the working directory, if one types:

purl("lob.rmd")

Exercises

1. Create an R Markdown document to contain your homework assignment. Modify the YAML header to allow numbering of figures and tables, but not sections. To test the formatting, perform the following steps:

   1. Create section header called Question 1 and a subsection header called (a). Under (a) type "completed".
   2. Under the subsection header (b), insert a chunk, and create a simple plot of points at the coordinates: \(\{1,1\}\), \(\{2,2\}\), \(\{3,3\}\), by typing the code: plot(1:3) in the chunk. Create a label for the chunk, and a create caption for plot using the knitr chunk option, fig.cap.
   3. Under the subsection header (c), create a cross reference for the plot from (b).
   4. Under the subsection header (d), write the equation, \(y_i = \hat{\beta}_0 + \hat{\beta}_1x_i + \hat{\varepsilon_i}\), using LaTeX. As noted earlier, a LaTeX equation cheatsheet can be found here.
   5. Render (knit) the final document as either an .html file or a .doc file. Include other assigned exercises for this Chapter as directed, using the general formatting approach given in Question 1.

2. Perform the following operations.

   1. Leave a note to yourself.
   2. Create and examine an object called x that contains the numeric entries 1, 2, and 3.
   3. Make a copy of x called y.
   4. Show the class of y.
   5. Show the base type of y.
   6. Show the attributes of y.
   7. List the current objects in your work session.
   8. Identify your working directory.

3. Distinguish R expressions and assignments.

4. Sometimes R reports unexpected results for its classes and base types.

   1. Create x <- factor("a","a","b") and show the class of x.
   2. Type ?factor. What is a factor in R?
   3. Show the base type of x? Is this surprising? Why? Type ?integer. What is an integer in R?

5. Solve the following mathematical operations using R.

   1. \(1 + 3/10 + 2\)
   2. \((1 + 3)/10 + 2\)
   3. \(\left(4 \cdot \frac{(3 - 4)}{23}\right)^2\)
   4. \(\log_2(3^{1/2})\)
   5. \(3\boldsymbol{x}^3 + 3\boldsymbol{x}^2 + 2\) where \(\boldsymbol{x} = \{0, 1.5, 4, 6, 8, 10\}\)
   6. \(4(\boldsymbol{x} + \boldsymbol{y})\) where \(\boldsymbol{x} = \{0, 1.5, 4, 6, 8\}\) and \(\boldsymbol{y} = \{-2, 0.5, 3, 5, 8\}\).
   7. \(\frac{d}{dx} \tan(x) 2.3 \cdot e^{3x}\)
   8. \(\frac{d^2}{dx^2} \frac{3}{4x^4}\)
   9. \(\int_3^{12} 24x + \ln(x)dx\)
   10. \(\int_{-\infty}^{\infty} \frac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}dx\) (i.e., find the area under a standard normal pdf).
   11. \(\int_{-\infty}^{\infty}\frac{x}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}dx\) (i.e., find \(E(X)\) for a standard normal pdf).
   12. \(\int_{-\infty}^{\infty}\frac{x^2}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}dx\) (i.e., find \(E(X^2)\) for a standard normal pdf).
   13. Find the sum, cumulative sum, product, cumulative product, arithmetic mean, median and variance of the data x = c(0, 1.5, 4, 6, 8, 10).

6. The velocity of the earth’s rotation on its axis at the equator, \(E\), is approximately 1674.364 km/h, or 1040.401 m/h¹⁷. We can calculate the velocity of the rotation of the earth at any latitude with the equation, \(V = \cos(\)latitude\(^\text{o}) \times E\). Using R, simultaneously calculate rotational velocities for latitudes of 0,30,60, and 90 degrees north, or south, latitude (they will be the same). Remember, the function cos() assumes inputs are in radians, not degrees.

References

Aho, Ken. 2014. Foundational and Applied Statistics for Biologists Using R. CRC Press.

Allaire, JJ, Yihui Xie, Christophe Dervieux, Jonathan McPherson, Javier Luraschi, Kevin Ushey, Aron Atkins, et al. 2024. Rmarkdown: Dynamic Documents for r. https://github.com/rstudio/rmarkdown.

Becker, Richard, JM Chambers, and AR Wilks. 1988. The New S Language. CRC Press.

Chambers, John M. 2008. Software for Data Analysis: Programming with R. Vol. 2. Springer.

Fox, John, and Sanford Weisberg. 2019. An R Companion to Applied Regression. Third. Thousand Oaks CA: Sage. https://socialsciences.mcmaster.ca/jfox/Books/Companion/.

Hershey, Allen V. 1967. Calligraphy for Computers. Vol. 2101. US Naval Weapons Laboratory.

Lin, Greg. 2023. Reactable: Interactive Data Tables for r. https://CRAN.R-project.org/package=reactable.

R Core Team. 2024a. R Internals. https://cran.r-project.org/doc/manuals/r-release/R-ints.html.

———. 2024b. R Language Definition. https://cran.r-project.org/doc/manuals/r-release/R-lang.html.

Venables, W. N., and B. D. Ripley. 2002. Modern Applied Statistics with S. Fourth Edition. New York: Springer. https://www.stats.ox.ac.uk/pub/MASS4/.

Wickham, Hadley. 2019. Advanced R. CRC press.

Xie, Yihui. 2015. Dynamic Documents with R and Knitr. 2nd ed. Boca Raton, Florida: Chapman; Hall/CRC. https://yihui.org/knitr/.

———. 2016. Bookdown: Authoring Books and Technical Documents with R Markdown. Boca Raton, Florida: Chapman; Hall/CRC. https://bookdown.org/yihui/bookdown.

———. 2023. Bookdown: Authoring Books and Technical Documents with R Markdown. https://github.com/rstudio/bookdown.

———. 2024. Tinytex: Helper Functions to Install and Maintain TeX Live, and Compile LaTeX Documents. https://github.com/rstudio/tinytex.

Xie, Yihui, Joseph J Allaire, and Garrett Grolemund. 2018. R Markdown: The Definitive Guide. Chapman; Hall/CRC.

Xie, Yihui, Joe Cheng, and Xianying Tan. 2024. DT: A Wrapper of the JavaScript Library ’DataTables’. https://CRAN.R-project.org/package=DT.

Xie, Yihui, Christophe Dervieux, and Emily Riederer. 2020. R Markdown Cookbook. CRC Press.

Zhu, Hao, T Travison, T Tsai, W Beasley, Y Xie, G Yu, S Laurent, R Shepherd, Y Sidi, et al. 2022. “kableExtra: Construct Complex Table with ‘Kable’ and Pipe Syntax. 2021.” URL Https://CRAN. R-Project. Org/Package= kableExtra. R Package Version 1 (1): 579.

---

1. Unix/Linux operating systems require R to be launched from the shell command line by typing: R. This will begin an interactive R session on the system shell command line itself.↩︎

2. A Unix/Linux GUI, similar to those in Windows and Mac OS, can be initiated by opening R with the commands: R -g Tk &.↩︎

3. Although we can view everything created or loaded in R as an object, not all R objects fit neatly into the OOP perspective of “object-oriented.” This is true because R base objects (which are not object oriented) come from S, which was developed before anyone considered the need for an S OOP system (see Wickham (2019) and Chambers (2008)).↩︎

4. There are many OOP languages including R, C#, C++, Objective-C, Smalltalk, Java, Perl, Python and PHP. C is not considered an OOP language.↩︎

5. Specifically, R base types correspond to an underlying C-codified typedef, i.e., an alias framework for C data types. This internal algorithm is referred to by by the R-core development team as SEXPTYPE, meaning S-expression (SEXP) type (R Core Team 2024a). There are currently 24 SEXPTYPE variants, each corresponding to one of the 24 R base types.↩︎

6. The functions mode() and storage.mode() are generally not appropriate for identifying R base types and storage modes (Wickham 2019). In particular, the function mode() gives the mode of an object with respect to the S3 system (see Becker, Chambers, and Wilks (1988)), whereas storage.mode() is generally used when interfacing with algorithms written in other languages, primarily C or Fortran, to check that R objects have the correct type for the interfaced language.↩︎

7. Chapter 10 provides instructions on how to develop documentation files for your own packages.↩︎

8. Importantly, the functions savehistory(), loadhistory(), and history() are not currently supported for Mac OS. There are ways around this. For instance, in RStudio (Section 2.9), the Mac OS command history can be obtained by clicking the History icon that appears on the tool bar at the top of the console window. As an additional issue, Windows and Unix-alike platforms have different implementations for savehistory() and loadhistory(). See help pages for these functions within your platform for particulars.↩︎

9. This command will not work in an embedded Windows R GUI, like the one in RStudio.↩︎

10. Other text editors with at least some IDE support for R include, but are not limited to, NppToR in Notepad++, Bluefish, Crimson Editor, ConTEXT, Eclipse, Vim, Geany, jEdit, Kate, TextMat, gedit, and SciTE.↩︎

11. On 7/27/2022 RStudio announced it was shifting to a new name, Posit, to acknowledge its growth beyond a simple IDE for R. The RStudio name will be retained for RStudio Desktop, and the RStudio Server, but it will be changed for other applications including the RStudio Workbench (now Posit Workbench) and the RStudio Package Manager (now Posit Package Manager).↩︎

12. Markdown is a highly flexible language for creating formatted text using a plain-text editor. HyperText Markup Language or HTML is the standard markup language for documents designed for web browser display.↩︎

13. YAML is a data serialization language. The YAML acronym was originally intended to mean “Yet Another Markdown Language,” but more recently has been given the recursive acronym: “YAML Ain’t Markup Language.” R Markdown uses the YAML format header to communicate with Pandoc, a document converter, written in the Haskell language, embedded in RStudio, with respect to desired document output↩︎

14. Pandoc can convert Markdown .md files, into many formats including, .rtf, .doc, and .pdf↩︎

15. Support for LaTeX can be found at the and at a large number of informal user-driven venues, including Stack Exchange and Overleaf, an online LaTeX application↩︎

16. The document you are reading was either knitted from an R Markdown .rmd file (using bookdown) or a Sweave .rnw file, created in RStudio.↩︎

17. The circumference of the earth at the equator is 40,075.02 km (24,901.5 mi). The earth completes one full rotation on its axis with respect to distant stars in 23 hours 56 minutes 4.091 seconds (a sidereal day). This means that in 24 hours, the earth rotates \(\frac{24}{23 + (56/60) + (4.091/60)/60} = 1.002738\) times. And this means that the velocity of the earth at the equator is \(\frac{1.002738 \times 40075.02}{24} = 1674.364\) k\(\cdot\)h\(^{-1}\), or \(0.621371 \times 1674.364 = 1040.401\) m\(\cdot\)h\(^{-1}\).↩︎