Chapter 8 Functions

“A computer will do what you tell it to do, but that may be much different from what you had in mind.”

- Joseph Weizenbaum, Important early software developer and AI ethisist

8.1 Introduction to Functions

In computer programming, a function is a set of instructions for performing a specific task, or providing specific output. Essentially all processes in R are run via functions. For example, the command: x <- 2, assigns the label x to the numeric value 2. This is actually accomplished, however, via the function `<-`. That is, one could rewrite the expression x <- 2 as:

`<-`(x, 2)
x

[1] 2

Similarly, summations are evaluated with the underlying function `+`.

`+`(2, 2)

[1] 4

Function call translations, for example, from 2 + 2 to `+`(2, 2), are made silently through the R-interpreter¹, which makes it unnecessary to compile R code into executable files (see Ch 9).

8.1.1 function() and Function Base Types

Generally speaking, an R function –at the risk of sounding repetitive– is a function defined by the function function() 🙂. Arguments in R functions will be contained in a set of parentheses in the call to function() itself. The function contents follow, generally delineated by curly brackets. Thus, we have the form:

function.name <- function(arg.1, arg.2,...., arg.n){function contents}

Recall from Chapter 2 that there are three R base types specific to functions: closure, special, and builtin. Functions of base types special and builtin are constrained to the base package, and include primitive functions built into the R system, and implemented in C. Types builtin and special can be distinguished as functions that do and do not evaluate their arguments, respectively (R Core Team 2024).

Example 8.1

The code below allows listing of R primitive functions (Chambers 2008). On Line 1, a character vector containing base functions named base.objs is generated using the function objects(). Strings from base.objs are used to test if the functions are primitive by using is.primitive() as the FUN argument in sapply(). Boolean outcomes from the test are used to subset base.objs into the object prim.objs.
\(\text{}\)

base.objs <- objects("package:base", all = TRUE)
prim.objs <- base.objs[sapply(base.objs, function(x) is.primitive(get(x)))]

The summarization is continued in the chunk below. On Line 1, the function split() used to split data in prim.objs into distinguishing base type categories using typeof(get()) within sapply() (Lines 2 and 3). Numbers of items in these groups are tabulated using sapply() again (Line 5). There are currently 168 builtin and 42 special primitive functions in R.

base.types <- split(prim.objs, 
                    sapply(prim.objs, 
                           function(x) typeof(get(x))))

sapply(base.types, length)

builtin special 
    168      42 

Here are the first 20 special primitive functions:

base.types$special[1:20]

 [1] "$"         "$<-"       "&&"        ".Internal" "::"       
 [6] ":::"       "@"         "@<-"       "["         "[["       
[11] "[[<-"      "[<-"       "{"         "||"        "~"        
[16] "<-"        "<<-"       "="         "break"     "call"     

Here are the first 20 builtin primitive functions:

base.types$builtin[1:20]

 [1] "-"                  "!"                  "!="                
 [4] "%%"                 "%*%"                "%/%"               
 [7] "&"                  "("                  "*"                 
[10] "...elt"             "...length"          "...names"          
[13] ".C"                 ".cache_class"       ".Call"             
[16] ".Call.graphics"     ".class2"            ".External"         
[19] ".External.graphics" ".External2"        

Clearly, primitive functions of base type special and builtin include conventional operators (with bounding accent grave characters). For example, `$` has base type special,

typeof(`$`)

[1] "special"

and `+` has base type builtin.

typeof(`+`)

[1] "builtin"

\(\blacksquare\)

Primitive functions generally make calls to the function .Primitive(), which identifies an underlying C routine used for evaluating the outer function. For example, we see that `+`, as codified in R, calls a C routine identified with "+".

`+`

function (e1, e2)  .Primitive("+")

8.1.2 Base Type closure

Primitive functions (those of types special and builtin) cannot be created by users outside of the R development core team. Thus, base type closure represents the only kind of function R-users can actually create and easily modify. The name “closure” refers to the programming style underlying these functions, with each assigned to a particular environment with local internal objects (see Section 5.4 in Chambers (2008)). Consider the simple homemade function square.me().

square.me <- function(x){
  x^2
}

square.me(4)

[1] 16

typeof(square.me)

[1] "closure"

Functions of base type closure will have three components.

• The formal arguments constitute the arguments that control the function. The formals can be accessed via the function formals(). For instance,

formals(square.me)

$x

The formals of a function will have a pairlist base type.

typeof(formals(square.me))

[1] "pairlist"

• The body constitutes the actual function code. The function body() returns the body of a function as an unevaluated expression.

body(square.me)

{
    x^2
}

• The environment is a base type that defines the data structure the function requires for its computations. An environment is required for all R functions, whether they are builtin, special, or closure. When an object assignment (including the naming of a function) occurs at the “top level” in an R session (e.g., outside of the body of a function), its environment will be the global environment. The global environment is maintained throughout a session and can be saved across sessions using, for instance, the function save.image() (Section 2.7.2). Environments of functions can be checked, created, or changed using the function environment().

The environment of square.me() is the global environment.

environment(square.me)

<environment: R_GlobalEnv>

As is the the environment of the session itself.

environment()

<environment: R_GlobalEnv>

In contrast, the environment for the function mean() is the base package.

environment(mean)

<environment: namespace:base>

Functions in base, including mean(), are accessible, because the base package namespace is loaded automatically (along with most of the R distribution packages) upon opening R.

isNamespaceLoaded("base")

[1] TRUE

Example 8.2 \(\text{}\)
As a biological example, we will create a function for calculating predicted sizes of biological populations under geometric growth. The geometric growth equation (Eq. (8.1)) is often used to represent population growth for a species with unlimited resources and non-overlapping generations:

\[\begin{equation} f(t) = N_0\lambda^t, \tag{8.1} \end{equation}\]

where: \(N_0 =\) initial number of individuals, \(\lambda =\) the geometric rate of increase, and \(t\) = the number of time intervals or generations. We have:

Geo.growth <- function(N.0, lambda, t){
  Nt <- N.0 * lambda^t
  Nt
}

Note that the function has three arguments: N.0, lambda, and t.

A function-user must specify each of these. The first line of code in the function body solves \(N_0\lambda^t\). Importantly, the second (last) line of body code specifies the object we actually want returned, Nt. Without a “return value” nothing will be returned by the function. If one requires multiple return objects, then one can place them in single suitable container like a list.

To increase clarity, one should place the first curly bracket on same line as the arguments, and place last curly bracket on its own line. Readability can also be improved with the use of tabs and spaces. Note that I have indented lines containing related operations. This distinguishes those lines from the first (argument) line and the end (return) line. Note also that spaces are placed after commas, and before and after operators, including the assignment operator. This is also good general practice for code writing².

Below we run the function for different values of N.0, lambda, and t.

Geo.growth(N.0 = 100, lambda = 1.2, t = 20)

[1] 3833.76

Geo.growth(N.0 = 30, lambda = 0.2, t = 3)

[1] 0.24

Geo.growth(N.0 = 30, lambda = 1, t = 3)

[1] 30

\(\blacksquare\)

8.2 Global vs. Local Variables

As noted in Ch 1, objects in R are lexically scoped, allowing distinctions of global and local variables. Global variables are objects that exist within the global environment and consequently are broadly accessible, whereas local variables are only accessible in particular settings. Objects defined within a function, including arguments, are (generally) local to that function, and thus are accessible only within the body of the function.

We see that the object N.t, which was defined in the last line of Geo.growth(), is local to that function, since it cannot be detected in the global environment³.

Nt

Error in eval(expr, envir, enclos): object 'Nt' not found

Global variables can be assigned in functions using the super-assignment operator, <<-, although I have found the need for this operator to be rare (but see Section 11.2.1).

Geo.growth <- function(N.0, lambda,t){
  Nt <<- N.0 * lambda^t
  Nt
}

g <- Geo.growth(N.0 = 30, lambda = 1, t = 3)
Nt

[1] 30

Example 8.3 \(\text{}\)
The apply family of functions for data management, including apply(), tapply(), sapply() and lapply() (Section 4.1.1) allow inclusion of user-defined functions (see Example 8.1 from earlier in this chapter). The function stan() below centers and scales (standardizes) outcomes. That is, each element in the dataset is subtracted from its mean, and divided by its standard deviation). We can call stan() within apply(), using the latter function’s third (FUN) argument.

stan <- function(x){
  (x - mean(x))/sd(x)
}

out <- apply(Loblolly[,1:2], 2, stan)

As a consequence of the transformation, columns in the object out will the same mean (zero), and the same variance (one)

apply(out, 2, mean) # zero with rounding error

      height          age 
1.668665e-16 1.850759e-17 

apply(out, 2, var)

height    age 
     1      1 

\(\blacksquare\)

Example 8.4 \(\text{}\)
Below is a function called stats() that will simultaneously calculate a large number of distinct summary statistics.

stats <- function(x, digits = 5){
  require(asbio)
  ds <- data.frame(statistics = round(c(length(x), min(x), max(x),
                                        mean(x), median(x), sd(x), var(x),
                                        IQR(x), sd(x)/sqrt(length(x)),
                                        kurt(x), skew(x)), digits))
  rownames(ds) <- c("n", "min", "max", "mean", "median", "sd",
                    "var", "IQR", "SE", "kurtosis", "skew")
  ds
}

Note that the function contains two arguments (Line one): a call to a numeric data vector, x, and the number of significant digits to be used in printing the output. Because digits has been given a default value (digits = 5), only the first argument needs to be specified by the user. The first line of code in the body of the function (Line 2) indicates that package asbio is required by the function (the package contains the functions asbio::skew() and asbio::kurt() for calculating the data skew and kurtosis, respectively. In Lines 3-8 a dataframe is created called ds. The dataframe has one column called statistics, that will contain numeric entries for eleven statistical summaries of x. The summaries are rounded to the number of digits specified in digits. Lines 7-8 define the row names of ds. These are the names of the statistics calculated by the function. The last line of code in the body (Line 9) prints ds.

We can readily apply stats() directly to a single numeric column.

stats(Loblolly[,1])

         statistics
n          84.00000
min         3.46000
max        64.10000
mean       32.36440
median     34.00000
sd         20.67360
var       427.39793
IQR        40.89500
SE          2.25568
kurtosis   -1.47347
skew       -0.06434

Or apply the function to multiple columns, for instance, by calling stats() within apply(). For instance:

apply(Loblolly[,c(1:2)],2,stats)

$height
         statistics
n          84.00000
min         3.46000
max        64.10000
mean       32.36440
median     34.00000
sd         20.67360
var       427.39793
IQR        40.89500
SE          2.25568
kurtosis   -1.47347
skew       -0.06434

$age
         statistics
n          84.00000
min         3.00000
max        25.00000
mean       13.00000
median     12.50000
sd          7.89998
var        62.40964
IQR        15.00000
SE          0.86196
kurtosis   -1.37375
skew        0.18925

\(\blacksquare\)

8.3 Useful Functions for Writing Functions

8.3.1 switch()

A useful tool for function writing is switch(). It evaluates and switches among user-designated alternatives which can be defined in a function argument.

Example 8.5 \(\text{}\)
The function below switches between five different estimators of location (i.e., estimators of a typical or central value from a sample). These are the sample mean, a trimmed mean (using 10% trimming), the geometric mean, the median, and Huber’s \(M\)-estimator. See Chapter 4 in Aho (2014) for details concerning these estimators.

location <- function(x, estimator){
  require(asbio)
  switch(estimator,
    mean = mean(x), # arithmetic mean
    trim = mean(x, trim = 0.1), # trimmed mean
    geo = exp(mean(log(x))), # geometric mean (use for means of rates)
    med = median(x), # median
    huber = huber.mu(x), # Huber M-estimator
    stop("Estimator not included"))
}

location(Loblolly[,2], "geo")

[1] 10.19824

location(Loblolly[,2], "trim")

[1] 12.76471

Important to the function above is the pairing of the estimator argument in the overall function (Line 1) and a call to estimator in the first argument of switch (Line 3). As a final component of switch we address the contingency that a location estimator is specified that is not codified in the function. This is done using the stop() function with an appropriate message (Line 9).

\(\blacksquare\)

8.3.2 match.arg()

It is possible to specify partial matching for argument designations using the function match.arg().

Example 8.6 \(\text{}\)
For instance, what if we knew (or only wanted to specify) the first couple letters in the location estimator options for the previous function, location()? We could specify a step like the following.

indices <- c("mean", "trim", "geo", "median", "huber")
method <- match.arg(estimator, indices)

This is incorporated into location() on Lines 3-4 below. Note also the change in the first argument of switch from estimator (Line 5), which may have incomplete spelling of a location estimator name, to method, which will contain the complete index names from index.

location <- function(x, estimator){
  require(asbio)
  indices <- c("mean", "trim", "geo", "median", "huber")
  method <- match.arg(estimator, indices)
  switch(method,
    mean = mean(x), # arithmetic mean
    trim = mean(x, trim = 0.1), # trimmed mean
    geo = exp(mean(log(x))), # geometric mean (use for means of rates)
    med = median(x), # median
    huber = huber.mu(x), # Huber M-estimator
    stop("Estimator not included"))
}

Now we could do something like:

location(Loblolly[,2],"t")

[1] 12.76471

location(Loblolly[,2],"h")

[1] 13

\(\blacksquare\)

8.3.3 ...

The triple dot (...) operator⁴ allows customization of existing functions within another function. Thus, it is useful for writing wrapper functions (functions whose chief purpose is customization of an embedded function).

Example 8.7 \(\text{}\)
Imagine you wished to create a wrapper for the function plot() that allowed simultaneous computation and customized plotting of a simple linear regression model. We could do something like:

plot.reg <- function(x, y, ...){
  reg <- lm(y ~ x)
  plot(x, y, ...)
  abline(reg)
}

The first two formal arguments x and y on line Line 1, establish plotting coordinates of points, and define the outcomes for the explanatory and response variables, respectively. The third argument is the triple dot operator (Line 1). In the first line in the body of the function (Line 2) we create a general linear regression model using the function lm(). Line 3 creates a plot and, importantly, calls the triple dot operator from the arguments in plot.reg(). This allows specification of any possible plot() arguments, as arguments within plot.reg(). For instance, in the usage of plot.reg() below, I specify the x and y axis labels, a plotting character type, and symbols colors (Fig 8.1). The last line of code (Line 4) plots the regression line.

with(Loblolly, plot.reg(age, height, pch = 19, col = as.numeric(Seed),
         ylab = "Height (ft)", xlab = "Age (yrs)"))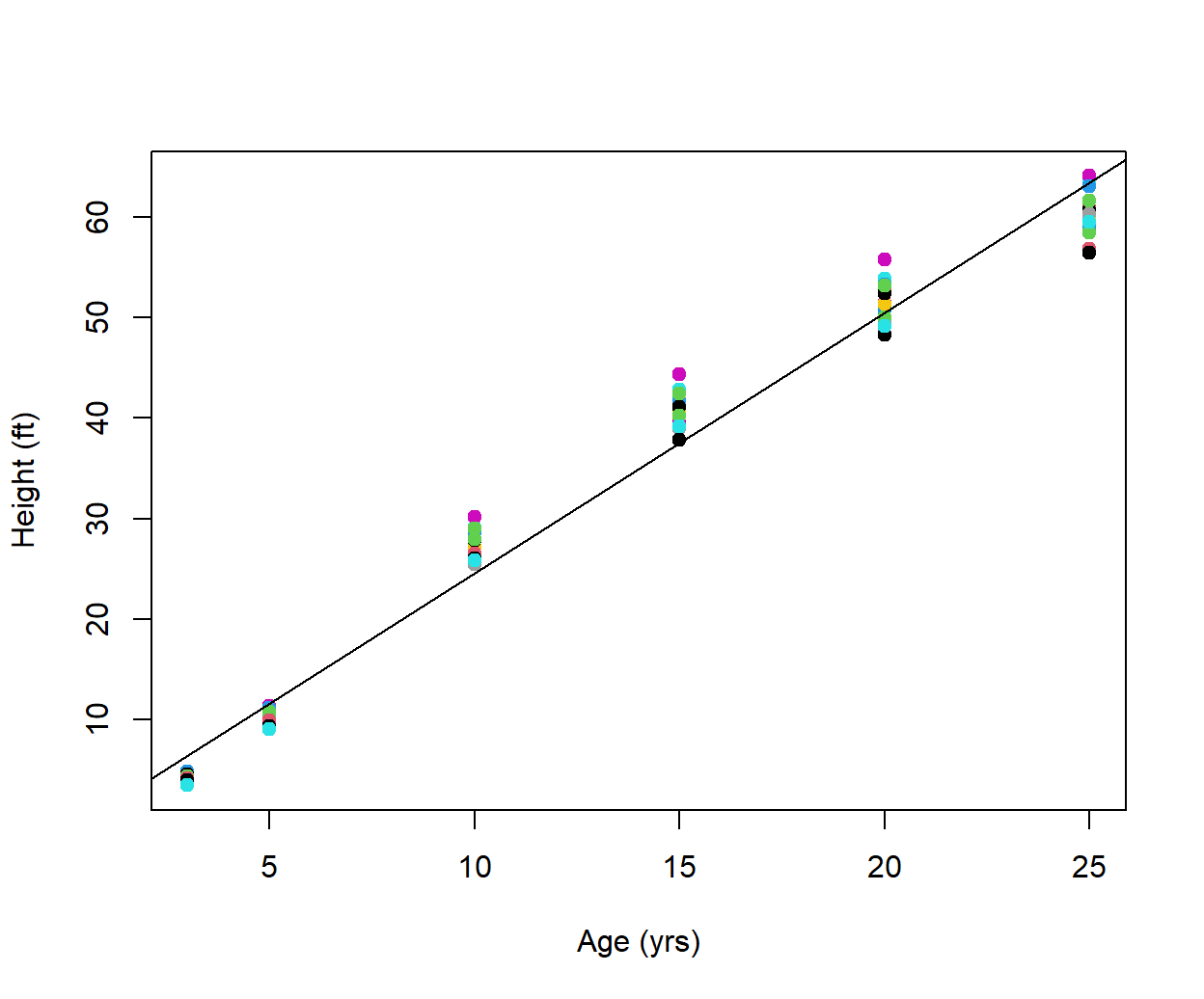

Figure 8.1: Representation of loblolly pine tree height as a function of age. Regression fit overlaid. Seed types are distinguished with colors.

\(\blacksquare\)

8.3.4 invisible()

The invisible() function can be useful when one wishes to have results computed and saved but not necessarily printed.

Example 8.8 \(\text{}\)
Assume that we want to retain plot.reg() as a plotting function, but wish to have potential access to actual statistical summaries from the regression model. We could rewrite plot.reg() as:

plot.reg <- function(x, y, plot = TRUE, ...){
  reg <- lm(y ~ x)
  if(plot){ plot(x, y, ...)
  abline(coef(reg))}
  invisible(summary(reg))
}

Note that I have added an argument, plot (Line 1), to control whether a plot is created via if(plot) (Line 3). By suppressing plotting I get no graphics (or text) output:

with(Loblolly, plot.reg(age, height, plot = FALSE))

However, if I assign a name to the function’s output, and print the assigned object, I get summary output for the regression model:

lob.model <- with(Loblolly, plot.reg(age, height, plot = FALSE))
lob.model

Call:
lm(formula = y ~ x)

Residuals:
    Min      1Q  Median      3Q     Max 
-7.0207 -2.1672 -0.4391  2.0539  6.8545 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) -1.31240    0.62183  -2.111   0.0379 *  
x            2.59052    0.04094  63.272   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 2.947 on 82 degrees of freedom
Multiple R-squared:  0.9799,    Adjusted R-squared:  0.9797 
F-statistic:  4003 on 1 and 82 DF,  p-value: < 2.2e-16

\(\blacksquare\)

8.4 Loops

Loop functions exist in some form in virtually all programming languages. A “for loop” in R is initiated using the function for(). The for construct requires a specification of three entities

• An index variable, e.g., i,
• The statement in
• A sequence that the index variable refers to as the loop commences.

Code defining the loop follows, generally delineated by curly brackets. In parallel to function writing it is good style to place the first curly bracket on the same line as the call to for, and to place the last curly bracket on its own line. Thus, we have the basic for loop format:

for(i in seq){
  loop contents
}

In the loop, values of index are used directly or indirectly to specify the \(i\)th element of something (e.g., matrix column, vector entry, etc.) as the for loop sequence commences. The replacement/definition process takes place in the “loop contents.” For instance,

for(i in 1:3){
  print(i)
}

[1] 1
[1] 2
[1] 3

8.4.1 Extending Scalar Arguments

One application for a loop is to make functions with scalar input arguments amenable to multi-element vector, matrix or dataframe inputs.

Example 8.9 \(\text{}\)
A library I created, plant.ecol, lives only on Github. We can access it with the code:

library(devtools)
install_github("moondog1969/plant.ecol")
library(plant.ecol)

The package devtools facilities building R packages from source code, and contains functions, e.g., install_github(), for downloading packages from unconventional repositories⁵. The function plant.ecol::radiation.heatl() calculates annual incident solar radiation (MJ cm\(^{-2}\) yr\(^{-1}\)) and heatload, a northern hemisphere thermal index that acknowledges that highest levels of heat loading occur on southwest facing slopes north of the equator. The function requires three arguments for some location of interest: slope, aspect, and north latitude, all measured in degrees.

formals(radiation.heatl)

$slope


$aspect


$lat

The function is designed to accommodate scalar inputs (single values for slope, aspect and lat). We will create a for loop to allow calculation of multiple values from a matrix. For instance, here are potential values for five sites.

envdata <- data.frame(slope = c(10, 12, 15, 20, 3),
                aspect = c(148, 110, 0, 30, 130),
                latitude = c(40, 50, 20, 25, 45))

We first create storage containers for the radiation and heatload results.

rad.out <- 1:nrow(envdata) -> hl.out

Here is a potential loop for our problem.

for(i in 1:length(rad.out)){
  temp <- with(envdata, radiation.heatl(slope[i],
                                         aspect[i],
                                         latitude[i]))
  rad.out[i] <- temp$radiation
  hl.out[i] <- temp$heat.load
}

The function was forced to loop around on itself letting i = 1 during the first loop, i = 2, during the second loop, up to i = 5 on the final loop. Here are the results.

cbind(rad.out, hl.out)

       rad.out    hl.out
[1,] 0.9976634 0.9455112
[2,] 0.8500810 0.7734540
[3,] 0.9302991 0.9668378
[4,] 0.8560357 0.8395667
[5,] 0.9185208 0.9001073

\(\blacksquare\)

8.4.2 Building on a Previous Result

Another application of a loop is to iteratively build on the results of the previous step(s) in the loop.

Example 8.10 \(\text{}\)
Consider the following function that counts the number of even entries in a vector of integers.

evencount <- function(x){
  res <- 0
  for(i in 1 : length(x)){
    if(x[i] %% 2 == 0) res <- res + 1
    }
  res
}

Recall from Ch 2 that %% is the modulus operator in R. That is, it finds the remainder in division. By definition the remainder of any even integer divided by two will be zero. At each loop iteration the function adds one to the numeric object res if the current integer in the loop is even (if it has remainder zero if divided by two).

evencount(1:3)

[1] 1

evencount(c(1,2,3,4,10))

[1] 3

\(\blacksquare\)

8.4.3 Summarizing Categorical Variables

A third loop application is the summarization of data with respect to levels in a categorical variable.

Example 8.11 \(\text{}\)
As an example we will create statistical summaries for height and age for each Seed type in the Loblolly dataset, using the stats function I created earlier. I first create an empty list to hold my result:

result <- list()

for(i in levels(Loblolly$Seed)){
    temp <- Loblolly[,1:2][Loblolly$Seed ==i,]
    result[[i]] <- as.data.frame(apply(temp, 2, stats))
    names(result[[i]]) <- c("Age","Height")
}

Loblolly$Seed. This is specified with: for(i in levels(Loblolly$Seed)). Note that on Line 2, the first two columns of the Loblolly dataset are subset by levels in Seed. Here are the results for seed type 305.

result$'305' # "name" of one of the 14 Loblolly seed types

               Age   Height
n          6.00000  6.00000
min        4.79000  3.00000
max       64.10000 25.00000
mean      35.11500 13.00000
median    37.30500 12.50000
sd        23.92709  8.60233
var      572.50563 74.00000
IQR       36.88500 12.50000
SE         9.76819  3.51188
kurtosis  -1.84795 -1.47809
skew      -0.16130  0.25449

\(\blacksquare\)

8.4.4 Looping Without for()

Looping in R is also possible using other general styles of Algol-like⁶ languages (e.g., C, C++, Pascal, and Fortran). This is accomplished with the constructs while(), repeat, and break.

Example 8.12 \(\text{}\)
Consider an example in which 2 is added to a base number until the updated number becomes greater than or equal to 10: We have:

i <- 1
while (i < 10) i <- i + 2
i

[1] 11

Or, to explicitly track the loop, we could use:

i <- 1; out <- i

while(TRUE){
    j <- i + 2
    out <- paste(out, j, sep = ",")
    i <- j
    if (i > 9) break
}

out

[1] "1,3,5,7,9,11"

Or, more simply

i <- 1; out <- i

repeat{
    j <- i + 2
    out <- paste(out, j, sep = ",")
    i <- j
    if (i > 9) break
}

out

[1] "1,3,5,7,9,11"

Here i took on values 1, 3, 5, 7, 9, and 11 as the loop commenced (this information is accumulated in the object out). When i equaled 11, the condition for continuation of the loop failed and the loop was halted.

CAUTION!

Some care should be exercised with while() and repeat since infinite loops will result if impossible breaks are specified.

\(\blacksquare\)

8.4.5 Final Looping Considerations

Despite their potential usefulness, loops can run slowly in R because it is an interpreted language (see Ch 9). Loops can often be avoided altogether. For example, one could rewrite the earlier evencount() function as:

evencounti <- function(x){
  out <- ifelse(x %% 2 == 0, 1, 0)
  sum(out)
}
# even outcomes from a random Poisson process
evencounti(rpois(1000, 2))

[1] 504

This increases efficiency, as documented by the function system.time():

system.time(evencount(1:1000000))

   user  system elapsed 
   0.19    0.02    0.20 

system.time(evencounti(1:1000000))

   user  system elapsed 
   0.03    0.01    0.05 

Loops can often be run more efficiently using the apply() family of functions (see animation examples using lapply() in Chs 6 and 7).

If loops are necessary, speed is an issue, and use of alternative approaches (e.g., lapply()) is awkward or suboptimal, one can call a compiled C, C++, or Fortran script from within R to run the loop. This topic is addressed further in Ch. 9.

8.5 Functional Programming

In functional programming one uses a declarative programming style that applies “pure” (often argument-less) functions⁷. Binary or infix operations require exactly two operands, and provide excellent examples of functional programming. The primitive functions `+`, `-`, `*` (Section 8.1) are binary operator functions. When more than two operands are supplied, the functions still work in pairs. Thus,

`+`(1,`+`(2,3))

[1] 6

is equivalent to

1 + 2 + 3

[1] 6

One can create personalized operator functions using the syntax: `% operator name %` or "% operator name %".

Example 8.14 \(\text{}\)
It might be useful to have an operator-style function for computing cumulative sums of individual numbers (although cumsum() does this already for numerical or complex objects). We will call our new operator %+%.

`%+%` <- function(a,b){c(a, a + cumsum(b))}

2.1 %+% 7.4

[1] 2.1 9.5

To make the operator work for more than two numbers, the second operand must be a multi-element numeric object.

2.1 %+% c(2.6, 1.5)

[1] 2.1 4.7 6.2

\(\blacksquare\)

Useful R functions for functional programming include Reduce(), Filter(), Find(), Map(), Negate(), and Position().

Example 8.15 \(\text{}\)
As a more applied example, recall from Section 4.2.8 that the %in% operator can be used to indicate if there is a match (or not) for its left operand. This does not clarify, however, how one might specify not %in%. The operations !%in% and %!in%, for example, do not work. The code below creates a %!in% operator using the function Negate().

`%!in%` <- Negate(`%in%`)

We apply `%!in%` below to subset bacterial phylum names.

big <- c("Abawacabacteria", "Absconditabacteria", "Acidobacteriota", 
         "Actinomycetota", "Aminicenantes", "Atribacterota", 
         "Aquificota", "Azambacteria")
small <- c("Acidobacteriota", "Actinomycetota")

w <- which(big %!in% small) 
big[w]

[1] "Abawacabacteria"    "Absconditabacteria" "Aminicenantes"     
[4] "Atribacterota"      "Aquificota"         "Azambacteria"      

\(\blacksquare\)

8.6 Functions with Classes and Methods

R object classes can have particular methods for plotting, printing, and summarization. Following a relatively simple series of steps, these methods can be implemented using generic function names, i.e., plot(), print(), summary(). For example, the function lm() creates objects of class lm.

model <- lm(height ~ age, data = Loblolly)
class(model)

[1] "lm"

There are specific summary, print, and plot methods for an object of class lm. Code for these methods can be viewed by typing stats:::summary.lm, stats:::print.lm, and stats:::plot.lm, respectively. The stats:::print.lm will be called automatically to print an object of class lm. For instance,

print(model)

Call:
lm(formula = height ~ age, data = Loblolly)

Coefficients:
(Intercept)          age  
     -1.312        2.591  

or, more simply,

model

Call:
lm(formula = height ~ age, data = Loblolly)

Coefficients:
(Intercept)          age  
     -1.312        2.591  

Here are 20 out of the more than 500 functions on my workstation that can be called with print, depending on the class of the object that is being printed.

methods(print)[1:20]

 [1] "print,ANY-method"            "print,diagonalMatrix-method"
 [3] "print,sparseMatrix-method"   "print.abbrev"               
 [5] "print.acf"                   "print.activeConcordance"    
 [7] "print.addtest"               "print.AES"                  
 [9] "print.agnes"                 "print.allPerms"             
[11] "print.anosim"                "print.anova"                
[13] "print.Anova"                 "print.anova.gam"            
[15] "print.anova.lme"             "print.anova.loglm"          
[17] "print.aov"                   "print.aovlist"              
[19] "print.ar"                    "print.Arima"                

Importantly, we are not limited to the pre-existing object classes in R (e.g., lm, numeric, factor, etc.). Instead, we can create user-defined classes for function output. These classes can also have methods for plotting, printing, and summarization.

8.6.1 S3 and S4

R has two-main approaches for developing OOP classes: S3, and S4^{8 9} Wickham (2019) notes:

“S3 allows your functions to return rich results with user-friendly display and programmer-friendly internals”

and

“S4 is a rigorous system that forces you to think carefully about program design. It’s particularly well-suited for building large systems that evolve over time and will receive contributions from many programmers.”

S3 methods tend to be easier to develop than S4 methods, and this approach is recommended for most applications in R. The amenability of S4 for interfacing with multiple programmers explains why this approach is required for contribution to the highly collaborative Bioconductor project. S4 OOP classes and their associated methods are implemented via the R-distribution package methods. I focus on S3 methods here, but briefly consider S4 methods.

8.6.1.1 S3

S3 classes are created using the function class().

ISU <- list(name = "Idaho State University", n.students = 12000,  
            founded = 1905)
class(ISU) <- "univ"
ISU

$name
[1] "Idaho State University"

$n.students
[1] 12000

$founded
[1] 1905

attr(,"class")
[1] "univ"

Note that the object ISU has the class attribute "univ". The sloop package contains functions to help distinguish OOP class frameworks. The function sloop::otype() can be used to determine if an object is S3, S4, RC, or R6.

library(sloop)
otype(ISU)

[1] "S3"

The object ISU is S3.

An S3 (or S4 object) is fairly useless without associated methods. Here is a simple print method for an object of class univ, i.e., a list with components: name, founded, and n.students.

print.univ <- function(x){
  cat(x$name, " was founded in ", x$founded, ",\nand has an enrollment of ",
      x$n.students, " students.", sep = "")
}

This dramatically changes the way the object ISU is printed.

ISU

Idaho State University was founded in 1905,
and has an enrollment of 12000 students.

Functions useful in creating print methods include cat() (used above) and structure(). The function cat() concatenates text into a single character vector, and prints the results. As a simple example, in the code below we bind the string ``iteration = '', to a random integer generated from a Poisson distribution rpois(1, 10), and apply a double line break .

cat("iteration = ", rpois(1, 10), "\n\n", sep = "")

iteration = 8

The function structure() allows one to assign an attribute set to data.

structure(.Data = 1:6, dim = 2:3)

     [,1] [,2] [,3]
[1,]    1    3    5
[2,]    2    4    6

structure(.Data = 1:6, names = LETTERS[1:6])

A B C D E F 
1 2 3 4 5 6 

We can identify methods specific to some class using the function sloop::ftype.

ftype(print.univ)

[1] "S3"     "method"

Example 8.16 \(\text{}\)
Here is a more complex example in which an output object from a function has an S3 class. The function asbio::pairw.anova is used for adjusting \(p\)-values resulting from multiple pairwise comparisons following an omnibus ANOVA (ANalysis Of VAriance). Objects generated by the function have class pairw and are S3.

eggs <- c(11,17,16,14,15,12,10,15,19,11,23,20,18,17,27,33,22,26,28)
trt <- factor(rep(1:4, c(5,5,4,5)))

tukey <- pairw.anova(y = eggs, x = trt)
class(tukey)

[1] "pairw"

otype(tukey)

[1] "S3"

Objects of class pairw have both print and plot methods.

ftype(print.pairw) # print method for class pairw

[1] "S3"     "method"

ftype(plot.pairw) # plot method for class pairw

[1] "S3"     "method"

The correct S3 method for a generic function call, e.g., print(), is identified using a process called method dispatch. Method dispatch steps in R are identifiable using the function sloop::s3_dispatch. Here is the process of identifying the correct printing method for an object of class pairw.

s3_dispatch(print(tukey))

=> print.pairw
 * print.default

Here is the actual print method’s output:

tukey

95% Tukey-Kramer confidence intervals 

         Diff     Lower    Upper  Decision Adj. p-value
mu1-mu2   1.2  -4.71976  7.11976    FTR H0     0.935298
mu1-mu3  -4.9 -11.17885  1.37885    FTR H0      0.15489
mu2-mu3  -6.1 -12.37885  0.17885    FTR H0     0.058287
mu1-mu4 -12.6 -18.51976 -6.68024 Reject H0     0.000101
mu2-mu4 -13.8 -19.71976 -7.88024 Reject H0      3.7e-05
mu3-mu4  -7.7 -13.97885 -1.42115 Reject H0     0.014218

This same method is used for other objects from asbio whose output has class pairw. These include objects from functions providing pairwise comparisons of factor levels following: an omnibus Friedman’s test¹⁰, pairw.fried(), and an omnibus Welch’s test¹¹, pairw.oneway().

welch <- pairw.oneway(y = eggs, x = trt)
welch

95% Welch adjusted confidence intervals 

         Diff     Lower    Upper  Decision Adj. p-value
mu1-mu2   1.2  -3.39503  5.79503    FTR H0      0.55425
mu1-mu3  -4.9    -8.991   -0.809    FTR H0     0.068803
mu2-mu3  -6.1 -11.06986 -1.13014    FTR H0     0.068803
mu1-mu4 -12.6 -17.53547 -7.66453 Reject H0    0.0032699
mu2-mu4 -13.8 -19.36022 -8.23978 Reject H0    0.0027003
mu3-mu4  -7.7 -12.95069 -2.44931 Reject H0      0.04229

\(\blacksquare\)

Viewing of code for S3 methods functions may require use of the double colon operator, e.g., asbio::plotpairw, or the triple colon operator, :::.

Example 8.17 \(\text{}\)
In this extended exercise we will fashion an advanced function, with an S3 class and create associated methods, using a number of approaches discussed so far in this chapter.

In ecological studies, \(\alpha\)-diversity measures the level of species evenness and richness within individual plots in a dataset. The most widely used alpha diversity indices are Simpson’s index, \(D_1\), and the Shannon-Weiner index, \(H'\).

\[\begin{equation} D_1 = 1 - \sum_{i=1}^S p_i^2 \tag{8.2} \end{equation}\]

\[\begin{equation} H' = -\sum_{i=1}^S p_i \ln p_i \tag{8.3} \end{equation}\]

where \(S\) denotes the number of species, and \(p_i\) is the proportional abundance of the \(i\)th species, \(i = 1,2,\ldots,S\).

Here are features I want my advanced \(\alpha\)-diversity function to have:

• Arguments specifying (1) a dataset for analysis, and (2) the type of \(\alpha\)-diversity we want calculated. So, two arguments.
• A function capable of handing summaries of communities for a single site, whose data will be a single numeric vector, and dataframes describing abundances of taxa at multiple sites.
• Assignment of correct names of sites (if any) to results.
• Partial matching of diversity method names using arg.match.
• An S3 class.
• Invisible components, appropriate for class print and plot methods.

alpha.div <- function(x, method = "simpson"){
  if(is.data.frame(x)) rn <- rownames(x) else {
    if(ncol(as.matrix(x) == 1)) rn = noquote("") else 
      rn = 1:nrow(as.matrix(x))
  }

  indices <- c("simpson", "shannon"); method <- match.arg(method, indices)

  x <- as.matrix(x)

  prop <- function(x){
      if(ncol(x) == 1) out <- x/sum(x)
      else
      out <- apply(x, 1, function(x) x/sum(x))
      out
    }

    p.i <- prop(x)

  simp <- function(x, p.i){
      if(ncol(x) == 1) D <- 1 - sum(p.i^2)
      else
      D <- 1 - apply(p.i^2, 2, sum)
      D
    }

  shan <- function(x, p.i){
      if(ncol(x) == 1) H <- -sum(p.i[p.i > 0] * log(p.i[p.i > 0]))
      else
      H <- apply(p.i, 2, function(x)-sum(x[x != 0] * log(x[x != 0])))
      H
    }

  div <- switch(method,
                simpson = simp(x, p.i),
                shannon = shan(x, p.i))

    out <- list(p.i = p.i, rn = rn, method = method, div = div)
  class(out) <- "a_div"; invisible(out)
}

Below is a breakdown of important components of the function alpha.div() above.

• In the arguments (Line 1), x is assumed to be either 1) a dataframe of taxa abundances at sites, with sites in rows (identified by row names) and taxa in columns, or 2) a numeric vector containing abundances of distinct taxa at a single site.
• In the first lines of code in the function body (Lines 2-4), the function attempts to obtain site names from x. If x is a dataframe, this is done using rn <- rownames(x). If x is a vector describing a single site, distinguishing site names is probably not important, hence the code rn = noquote("").
• The alpha.div() function contains three sub-functions: prop() (Lines 11-16), which allows computation of \(p_i\), and is used to create the object p.i, simp() (Lines 20-25), which calculates Simpson’s diversities, and shan() (Lines 27-32), which calculates Shannon-Weiner diversities. The latter function contains exception handling steps for taxa abundances of zero which will be undefined in Eq (8.3). For instance, p.i[p.i > 0] on Line 28, and x[x != 0] on Line 30.
• Partial matching of diversity method names (i.e., "simpson" and "shannon") is facilitated through the function match.arg().
• Switching of diversity methods is done via switch() (Lines 34-36).
• The function output is a list named out, which contain four objects: the proportional abundances of taxa, the rownames of x (i.e, the site names), the diversity method used, and the actual calculated diversities (Line 38).
• In the last line of body code, out is assigned to the user-defined class a_div and made invisible.

Here we apply the function to the dataset varespec from the library vegan.

library(vegan)
data(varespec)
v.div <- alpha.div(varespec)
class(v.div)

[1] "a_div"

otype(v.div)

[1] "S3"

Printing the output object v.div results in a rather messy rendering of a list, prompting the creation of an a_div print method. Our print.a_div() function will succinctly and effectively summarize results from alpha.div while allowing access to additional (invisible) information.

Our function for printing can be relatively simple.

print.a_div <- function(x, digits = 5){
  method <- ifelse(x$method == "simpson", "Simpson",
                   "Shannon-Weiner")
  cat(method, " diversity:", "\n", sep = "")
  rq <- structure(x$div,  names = x$rn)
  print(rq, digits = digits)
  invisible(x)
}

• The required argument, x in print.a_div (Line 1), will be an object of class a_div, created by the function alpha.div(), e.g., the object v.div. Recall that this is a list containing multiple objects.
• The object x$method is used create a tidy text summary of the diversity method used (Lines 2-3). This string is combined with a another string and printed with a line break in: cat(method, " diversity:", "\n", sep = "")}` (Line 4).
• The actual diversities are printed with the help of the function structure() on Lines 5-6.

print(v.div)

Simpson diversity:
     18      15      24      27      23      19      22      16      28 
0.82171 0.76276 0.78101 0.74414 0.84108 0.81819 0.80310 0.82477 0.55996 
     13      14      20      25       7       5       6       3       4 
0.81828 0.82994 0.84615 0.83991 0.70115 0.56149 0.73888 0.64181 0.78261 
      2       9      12      10      11      21 
0.55011 0.49614 0.67568 0.50261 0.80463 0.85896 

Output from alpha.div() can also be used for plotting. Here is a plot function for objects of class a_div.

plot.a_div <- function(x, plot.RAC = FALSE){
  require(ggplot2)
  margin_theme <- function(){
  theme(axis.title.x = element_text(vjust=-5),
        axis.title.y = element_text(vjust=5),
        plot.margin = margin(t = 7.5, r = 7.5,
                             b = 20, l = 15))
  }

  ptype1 <- function(){
  spi <- apply(x$p.i, 2, function(x)sort(x, decreasing = TRUE))
  sspi <- data.frame(p.i = stack(as.data.frame(spi))[,1])
  sspi$Rank <- rep(1:nrow(x$p.i), ncol(x$p.i))
  sspi$Site <- rep(x$rn,  each = nrow(x$p.i))
    ggplot(sspi, aes(y = p.i, x = Rank, group = Site)) +
      geom_line(aes(y = p.i, x = Rank, colour = Site), alpha = .4) +
      ylab(expression(italic(p[i]))) +
      theme_classic() + margin_theme()
  }

  ptype2 <- function(){
      diversity <- data.frame(div =  x$div, Site = factor(x$rn))
      method <- ifelse(x$method == "simpson", "Simpson diveristy",
                   "Shannon-Weiner diveristy")
      ggplot(diversity) +
      geom_bar(aes(y = div, x = Site, fill = div), show.legend = FALSE,
               stat = "identity") +
      theme_classic() +
      margin_theme() +
      ylab(method) + xlab("Site")
  }
  if(plot.RAC)  ptype1() else ptype2()
}

• The plot method allows the creation of two distinct types of ggplots by calling distinct sub-functions, ptype1() and ptype2() via the argument plot.RAC (Line one).
• Barplots of site diversities are produced by using the default plot.RAC = FALSE which will run the function ptype2() on Lines 21-31 (Fig 8.2)
• Rank abundance curves (RACs) are created by specifying plot.RAC = TRUE which runs the function ptype1() on Lines 10-19 (Fig 8.3). RAC plots allow graphical expressions of both taxa richness and evenness, and may even provide insights regarding resource exploitation in community (Magurran 1988).

plot(v.div)

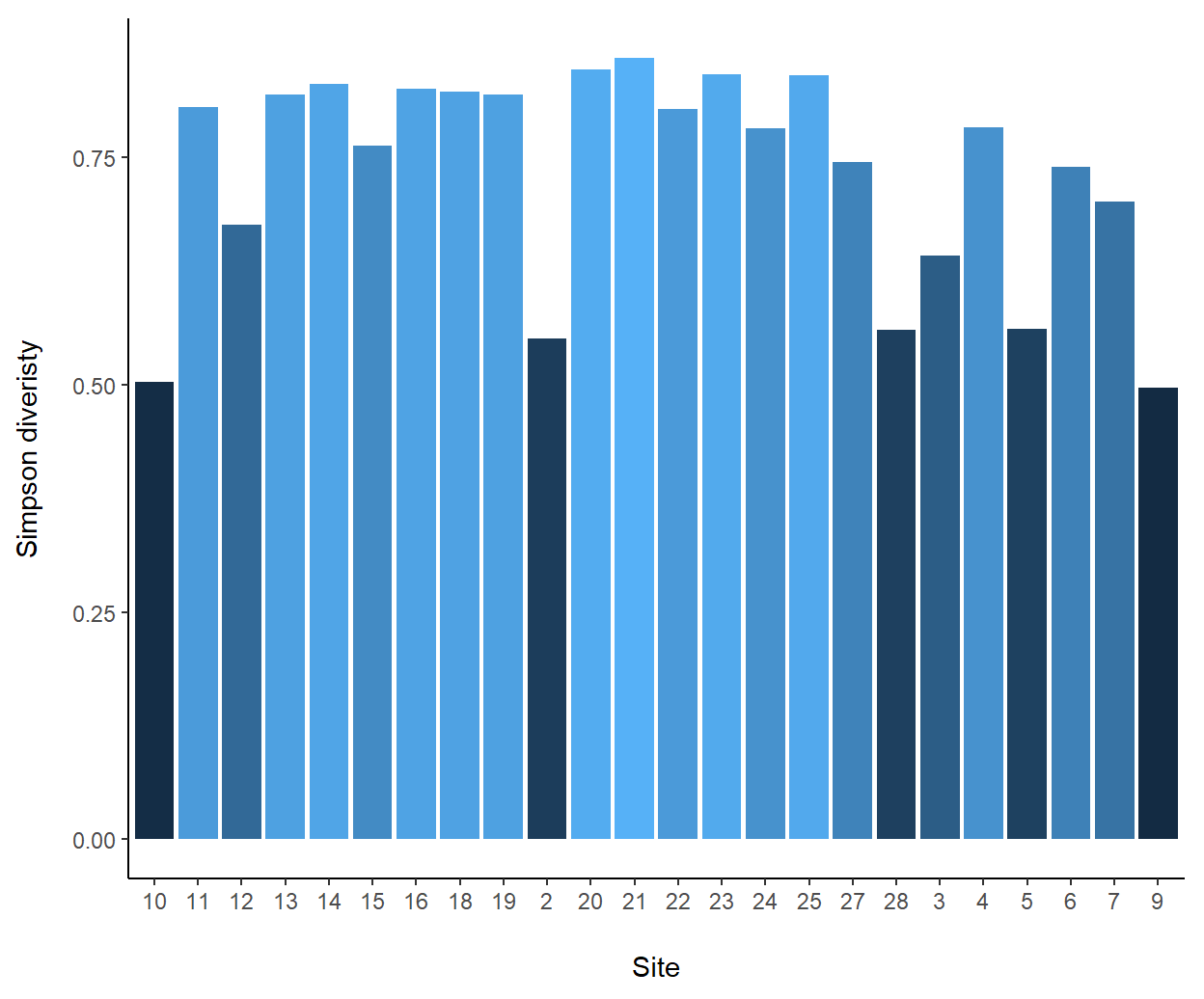
Figure 8.2: Barplot of site diversities from the vegan::varespec data. Note that bar colors are varied using the diversities themselves, i.e., fill = div.

plot(v.div, plot.RAC = TRUE)

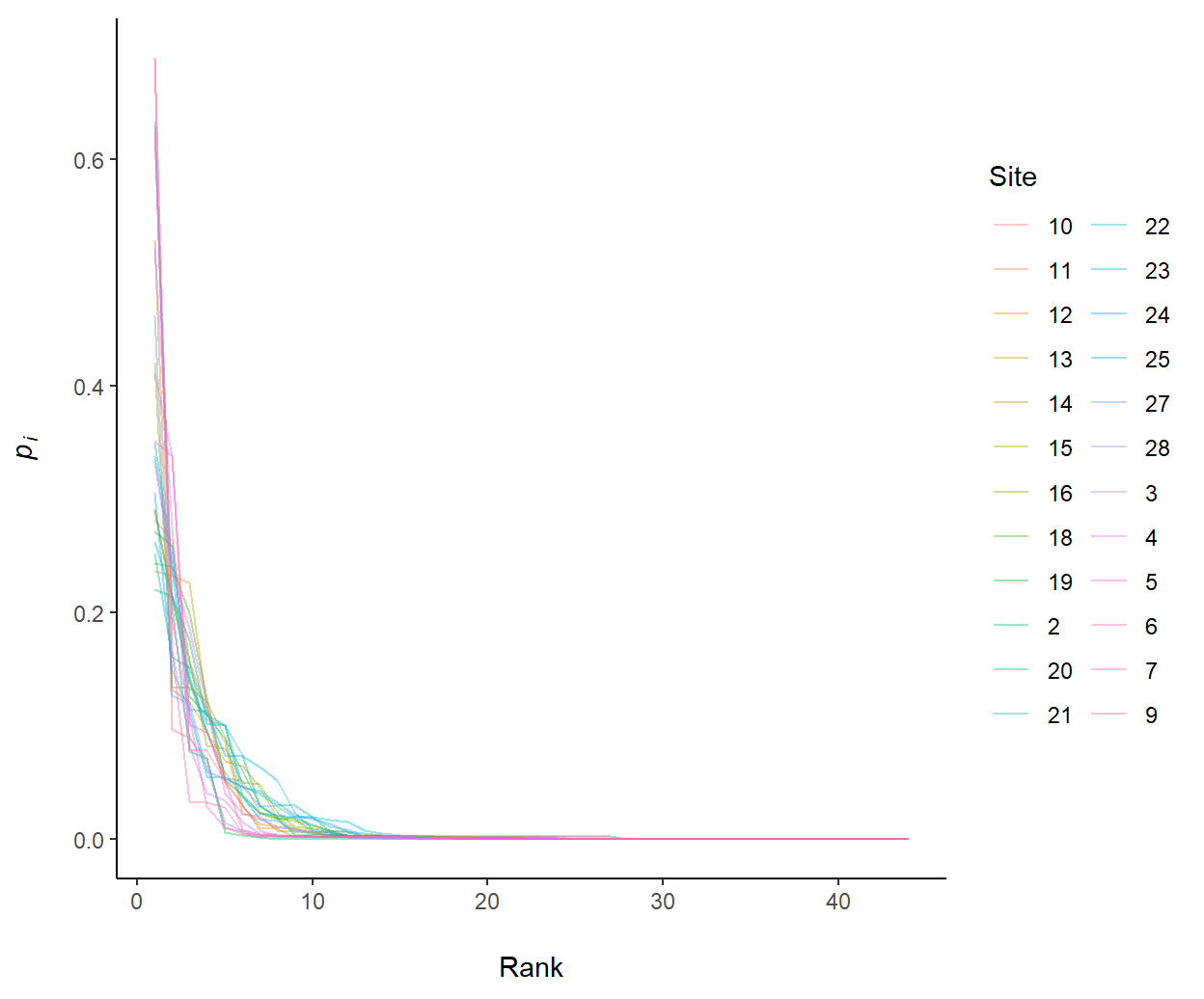
Figure 8.3: Rank abundance curves of the vegan::varespec dataset. Line lengths indicate species richness. Larger negative slopes indicate less species evenness.

\(\blacksquare\)

8.6.1.2 S4

An S4 class is defined using the function setClass(). Unlike S3 objects and classes, S4 class components, i.e., slots, must be defined in setClass(), along with the sub-classes of those components. Here I create an S4 class called univ for comparison to the S3 class univ created in the previous section.

setClass("univ", slots = list(name = "character", n.students = "numeric",
                              founded = "numeric"))

The S4 class univ will have three slots: name, n.students, and founded. S4 objects are created using the new() function.

ISU <- new(Class = "univ", name = "Idaho State University", 
           n.students = 12000, founded = 1905)

The object ISU has the S4 class univ.

class(ISU)

[1] "univ"
attr(,"package")
[1] ".GlobalEnv"

otype(ISU)

[1] "S4"

Here is the structure of the object:

str(ISU)

Formal class 'univ' [package ".GlobalEnv"] with 3 slots
  ..@ name      : chr "Idaho State University"
  ..@ n.students: num 12000
  ..@ founded   : num 1905

Just as components of a list are accessed using $, the slots of an S4 object are accessed using @.

ISU@founded

[1] 1905

Or with the function slot().

slot(ISU, "founded")

[1] 1905

We set S4 methods using the function setMethod(). Here is an S4 show() method (analogous to S3 print()) for objects of class univ.

setMethod("show",
"univ",
function(object) {
 cat(object@name, "was founded in", object@founded, 
     "and has an enrollment of",
     object@n.students, "students.", sep = " ")
}
)

ISU

Idaho State University was founded in 1905 and has an enrollment of 12000 students.

Example 8.18 \(\text{}\)
As a real-world S4 example, the function stats4::mle() estimates parameters for probability density functions using the method of maximum likelihood. Below we estimate the rate parameter for a Poisson distribution, \(\lambda\), based on a sample of count data.

# count data
y <- c(26, 17, 13, 12, 20, 5, 9, 8, 5, 4, 8)

# MLE for lambda in a Poisson distribution given data in y
nLL <- function(lambda) - sum(dpois(y, lambda, log = T))
# mle finds negative log-likelihoods
fit0 <- stats4::mle(nLL, start = list(lambda = 5),
                    nobs = length(y))

The MLE for the Poisson rate parameter, from data outcomes in y, is approximately 11.545. Notably, this is equal to the sample mean of y.

fit0

Call:
stats4::mle(minuslogl = nLL, start = list(lambda = 5), nobs = length(y))

Coefficients:
  lambda 
11.54545 

mean(y)

[1] 11.54545

The class of fit0 is mle. The class has an S4 designation.

class(fit0)

[1] "mle"
attr(,"package")
[1] "stats4"

otype(fit0)

[1] "S4"

The slot structure of an object from class mle is complex:

str(fit0)

Formal class 'mle' [package "stats4"] with 10 slots
  ..@ call     : language stats4::mle(minuslogl = nLL, start = list(lambda = 5), nobs = length(y))
  ..@ coef     : Named num 11.5
  .. ..- attr(*, "names")= chr "lambda"
  ..@ fullcoef : Named num 11.5
  .. ..- attr(*, "names")= chr "lambda"
  ..@ fixed    : Named num NA
  .. ..- attr(*, "names")= chr "lambda"
  ..@ vcov     : num [1, 1] 1.05
  .. ..- attr(*, "dimnames")=List of 2
  .. .. ..$ : chr "lambda"
  .. .. ..$ : chr "lambda"
  ..@ min      : num 42.7
  ..@ details  :List of 6
  .. ..$ par        : Named num 11.5
  .. .. ..- attr(*, "names")= chr "lambda"
  .. ..$ value      : num 42.7
  .. ..$ counts     : Named int [1:2] 14 8
  .. .. ..- attr(*, "names")= chr [1:2] "function" "gradient"
  .. ..$ convergence: int 0
  .. ..$ message    : NULL
  .. ..$ hessian    : num [1, 1] 0.953
  .. .. ..- attr(*, "dimnames")=List of 2
  .. .. .. ..$ : chr "lambda"
  .. .. .. ..$ : chr "lambda"
  ..@ minuslogl:function (lambda)  
  .. ..- attr(*, "srcref")= 'srcref' int [1:8] 5 8 5 56 8 56 5 5
  .. .. ..- attr(*, "srcfile")=Classes 'srcfilecopy', 'srcfile' <environment: 0x00000247766c5858> 
  ..@ nobs     : int 11
  ..@ method   : chr "BFGS"

\(\blacksquare\)

8.7 Advanced Biometric Examples

Customized R functions can be used to provide straightforward solutions of complex mathematical procedures associated with biological research.

Example 8.19 \(\text{}\)
Biologists often need to solve systems of dependent differential equations in models describing the propagation of electrochemical signals via action action potentials in neurons (Hodgkin and Huxley 1952), or models involving species interactions (e.g., competition or predation). For instance, the Lotka-Volterra competition model has the form:

\[\begin{equation} \begin{split} \frac{dN_1}{dt} &= r_{max1}N_1\frac{K_1-N_1-\alpha_{12}N_2}{K_1}\\ \frac{dN_2}{dt} &= r_{max2}N_2\frac{K_2-N_2-\alpha_{21}N_1}{K_2} \end{split} \tag{8.4} \end{equation}\]

where \(t\) denotes time, \(r_{max1}\) is the maximum per capita rate of increase (empirical rate) for species 1, and \(r_{max2}\) is the empirical rate for species 2, \(N_1\) and \(N_2\) are the number of individuals from species 1 and 2, respectively, \(K_1\) = the carrying capacity for species 1, i.e., the maximum population size for that species, \(K_2\) = the carrying capacity for species 2, \(\alpha_{12}\) is the competitive effect of species 2 on the growth of species 1, and \(\alpha_{21}\) is the competitive effect of species 1 on the growth rate of species 2.

We first bring in the package deSolve, which contains functions for solving ordinary differential equations (ODEs).

library(deSolve)

We then define starting values for \(N_1\) and \(N_2\) and model parameters.

xstart <- c(N1 = 10, N2 = 10)
pars <- c(r1 = 0.5, r2 = 0.4, K1 = 400, K2 = 300, a2.1 = 0.4,
             a1.2 = 1.1)

Next, we specify the Lotka-Volterra equations as a function. We will include the argument time = time even though it is not explicitly used in the function. This is required by ODE evaluators from deSolve.

LV <- function(time = time, xstart = xstart, pars = pars){
  N1 <- xstart[1]
  N2 <- xstart[2]
    with(as.list(pars),{
    dn1 <- r1 * N1 * ((K1 - N1 - (a1.2 * N2))/K1)
    dn2 <- r2 * N2 * ((K2 - N2 - (a2.1 * N1))/K2)
    res <- list(c(dn1, dn2))
    })
}

The most complex part of the function occurs on Lines 4-8 where the system of ODEs in Eq (8.4) is solved. Note the use of with() to make the components of the object pars accessible between braces on lines four and eight.

The deSolve::rk4() function solves simultaneous differential equations using classical Runge-Kutta 4th order integration (Butcher 1987)¹². The arguments for rk4() are, in order, the initial population numbers from species 1 and 2, the time frames to be considered, the function to be evaluated, and the parameter values.

out <- as.data.frame(rk4(xstart, time = 1:200, LV, pars))

The object out contains the number of individuals in species 1 and 2 (\(N_1\) and \(N_2\)) for time frames 1-200 (Fig 8.4).

plot(out$time, out$N2, xlab = "Time", ylab = "Number of individuals",
     type = "l")
lines(out$time, out$N1, type = "l", col = "red", lty = 2)
legend("bottomright", lty = c(1, 2), legend = c("Species 2", "Species 1"),
col = c(1, 2))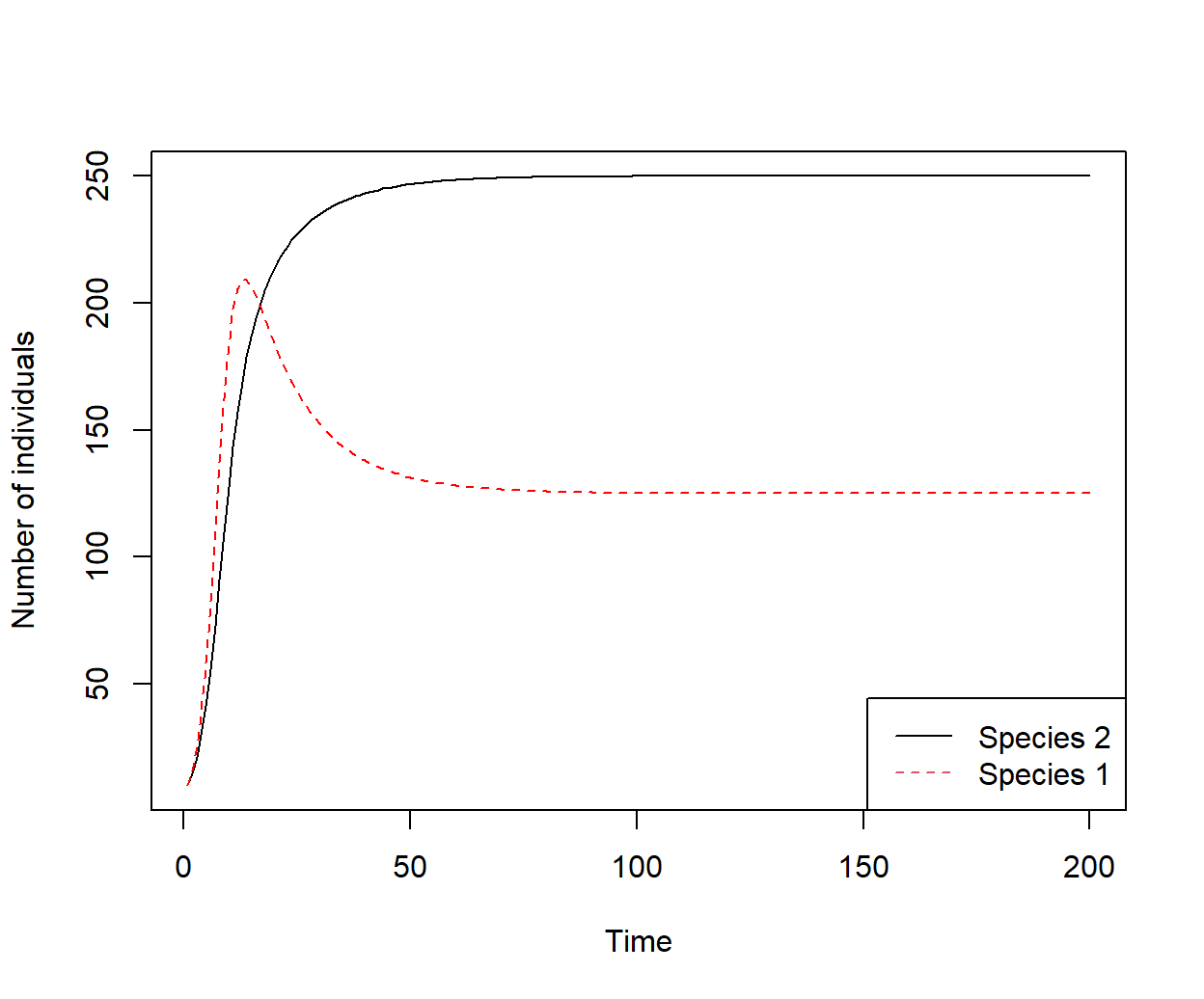

Figure 8.4: Solutions from Lotka Volterra ODEs for \(t = \{1, 2, ..., 200\}\). Species 1 and 2 coexist, but at levels appreciably below their carrying capacities as a result of interspecific competition.

\(\blacksquare\)

Example 8.20 \(\text{}\)
Parameter estimation in biostatistics often requires optimization of mathematical functions (finding function minima and maxima). A useful function for this application is uniroot(), which searches an interval for the zero root of a function. For instance, many location estimators (those which estimate “central” or “typical” values, e.g., estimators of the true underlying mean) will be the zero root the function: \[\begin{equation} \sum_{i = 1}^n(x_i - \hat{\mu}) \tag{8.5} \end{equation}\]

where \(x_i\) is the \(i\)th observation from a dataset, and \(\hat{\mu}\) is an estimator of a true location value. We will use uniroot() to find a location estimate that provides a zero root for this function.

As data we will use tree heights from the dataframe loblolly.

data <- Loblolly$height
f <- function(x) sum(data - x)
uniroot(f, c(min(data), max(data)))$root

[1] 32.3644

This value is identical to the sample mean of the tree heights.

mean(data)

[1] 32.3644

Indeed, the sample mean will be always be the zero root of Eq. (8.5). Normally the differences of the data points and the location estimate are squared, preceding summation. Minimizing this function is the process of ordinary least squares.

\(\blacksquare\)

8.8 The Process of Function Evaluation in R

Under construction ### Promises

Exercises

1. Divide the plant height and soil N values from the dataset from Q. 3 in the Exercises for Chapter 3 (the first two columns of the dataset) by their respective column sums by specifying an appropriate function as the 3rd argument for apply().

2. Below is McIntosh’s index of site biodiversity (McIntosh 1967): \[U = \sqrt{\sum_{i = 1}^s n_i^2}\] where \(s\) is the total number of species from a particular site, and \(n_i\) is the number of individuals from the \(i\)th species, \(i = 1,2,3,\ldots s\), from that site.

   1. Write a function to calculate the index.
   2. Check it by running it on the following collection of \(n_is\) obtained from a single site: ni <- c(5,4,5,3,2).

3. Below is the Satterthwaite formula for approximating degrees of freedom for the \(t\) distribution, under heteroscedasticity. \[\frac{\left(\frac{S_x^2}{n_x} + \frac{S_y^2}{n_y}\right)^2}{\frac{\left(S^2_x/n_x\right)^2}{n_x-1}+\frac{\left(S^2_y/n_y\right)^2}{n_y-1}}\] where \(S^2_x\) is the sample variance for variable \(x\), \(S^2_y\) is the sample variance for variable \(y\), \(n_x\) is the sample size for \(x\), and \(n_y\) is the sample size for \(y\).

   1. Write a function for this equation that has the variables \(x\) and \(y\) as arguments.
      
   2. Test the function for x <- c(1,2,3,2,4,5) and y <- c(2,3,7,8,9,10,11).

4. Create a function, implementing switch(), that can calculate the first or second derivative of a mathematical expression with respect to "x". Test it on x^3.

5. Create a function that calculates trimmed means for columns in a quantitative matrix or dataframe. Within the function, use the triple dot operator as an argument in mean(), to allow: 1) user-defined trimming (trim is an argument in the function mean()), and 2) user-defined handling of NA outcomes (na.rm is also an argument in mean()). Your function should have two arguments: one for input data, and one for the triple dot operator, ... . Test the function on the first two columns of asbio::cliff.sp. In your test specify both 10% trimming, and the removal of missing values.

6. Here are some classic computer science loop applications.

   1. A sequence of Fibonacci numbers is based on the function: \[\begin{align*} f(n) &= f(n-1) + f(n-2) \text{ for } n > 2\\ f(1) &= f(2) = 1 \end{align*}\] where \(n\) represents the \(n\)th step in the sequence. Using a loop, create the first 100 numbers in the sequence, i.e., find \(f(1)\) to \(f(100)\). As a check, the first five numbers in the sequence should be: 1, 1, 2, 3, 5.
   2. An interesting chaotic recursive sequence has the function: \[\begin{align*} f(n) &= f(n- f(n - 1)) + f(n - f(n-2)) \text{ for } n > 2\\ f(1) &= f(2) = 1 \end{align*}\] Using a loop, create the first 100 numbers in the sequence, i.e., find \(f(1)\) to \(f(100)\). As a check, the first five numbers in the sequence should be: 1, 1, 2, 3, 3.

7. Create an R animation by creating a for loop 360 steps long that changes the font-size, color, and string rotation of your name (as a character string) in an otherwise empty plot. Assuming the index i is used, your loop should include something resembling the code:

   plot(1:10, type = "n")
   text(5.5, "your name", cex = i/36, srt = i, col = i)
   Sys.sleep(0.1)

8. The Stirling number of the second kind (or the Stirling partition number) counts the number of ways a set of \(n\) objects can be partitioned into \(k\) groups. This is generally denoted \(S(n,k)\) or \(\left\{n \atop k \right\}\), and is calculated as:

\[\left\{n \atop k \right\} = \sum_{i=0}^k \frac{(-1)^{k-i} i^n}{(k-i)!i!}.\]

         Write a function that calculates \(\left\{n \atop k \right\}\) without using a for loop.
         Use the form: stirling2 <- function(n, k){function contents}.

9. The Bell number, \(B_n\), counts the number of ways a set with \(n\) elements can be partitioned (Bell 1938). That is, \(B_n\) will be the sum of Stirling numbers for a particular set, for \(k = \{1,2,\ldots,n\}\):

\[B_n = \sum_{k=1}^n \left\{{n\atop k}\right\}.\]

         Write a function for calculating \(B_n\) that uses stirling2, from Q 8, in a for loop.
         Use the form: belln <- function(n){function contents}.

10. The exercise below concerns the speed of loops in R. Use tapply() to simultaneously find the mean estimates of Loblolly$height for each level in Loblolly$seed, with and without a loop, and find the run times of the operations using system.time(). That is, run the following chunks:

    system.time(tapply(Loblolly$height, Loblolly$Seed, mean))

    out <- 1:nlevels(Loblolly$Seed)
    system.time(for(i in levels(Loblolly$Seed)){
      temp <- Loblolly[Loblolly$Seed == i,]
      out[i] <- mean(temp$height)
    })

    Describe and discuss your results.

11. Write a function to solve the systems of ODEs below \[\begin{align*} \frac{dx}{dt} &= ax + by\\ \frac{dy}{dt} &= cx + dy \end{align*}\] To test the function, let \(a = 3\), \(b = 4\), \(c = 5\), \(d = 6\), and solve for for \(t = 1,2,\ldots,20\), using classical Runge-Kutta 4\(^\text{th}\) order integration, as implemented by the function deSolve::rk4. Initial values for \(x\) and \(y\) can be anything but \(\{0,0\}\).

12. Make output from the function in previous question have an S3 class, and create a plotting method for objects of this class.

References

Aho, Ken. 2014. Foundational and Applied Statistics for Biologists Using R. CRC Press.

Bell, Eric Temple. 1938. “The Iterated Exponential Integers.” Annals of Mathematics 39 (3): 539–57.

Butcher, John Charles. 1987. The Numerical Analysis of Ordinary Differential Equations: Runge-Kutta and General Linear Methods. Wiley-Interscience.

Chambers, John M. 2008. Software for Data Analysis: Programming with R. Vol. 2. Springer.

Hodgkin, Alan L, and Andrew F Huxley. 1952. “A Quantitative Description of Membrane Current and Its Application to Conduction and Excitation in Nerve.” The Journal of Physiology 117 (4): 500.

Magurran, Anne E. 1988. Ecological Diversity and Its Measurement. Princeton University Press.

McIntosh, Robert P. 1967. “An Index of Diversity and the Relation of Certain Concepts to Diversity.” Ecology 48 (3): 392–404.

R Core Team. 2024. R Language Definition. https://cran.r-project.org/doc/manuals/r-release/R-lang.html.

Wickham, Hadley. 2019. Advanced R. CRC press.

---

1. Chambers (2008) describes function evaluation as a three step process: read \(\rightarrow\) parse \(\rightarrow\) evaluate, and refers to the programmatic mechanisms underlying this process as the R-evaluator.↩︎

2. A good R style guide can be found at: (https://google.github.io/styleguide/Rguide.html).↩︎

3. Commonly reported errors for functions using tidyverse code are given at the A future for R website.↩︎

4. This operator is not the same as the C-internal ... base type (Section 2.3.4).↩︎

5. Functions from the tidyverse package usethis will be useful for setting up passwords and tokens necessary for downloading from some repositories, including Github.↩︎

6. Algol (Algorithmic language) computer languages arose in the late 1950s from the language ALGOL 68. Important examples include Pascal, C, and Fortran.↩︎

7. Famous functional programming languages include Lisp, Scheme, F#, and Haskell.↩︎

8. S1 and S2 OOP classes do not exist. S3 and S4 were named according to the versions of S that they accompanied. S versions 1 and 2 didn’t have an OOP framework.↩︎

9. Wickham (2019) discusses two other less widely-used approaches: RC and R6. RC, or Reference Classes, are generated using the base function setRefClass(). Approaches for generating R6 objects and classes are provided by the R6 package, and are more similar to RC than to S3 and S4.↩︎

10. Friedman’s test is a non-parametric alternative to an ANOVA with a blocking variable.↩︎

11. Welch’s test, implemented using oneway.test, allows heteroscedasticity among factor levels when comparing factor level means.↩︎

12. The method of Euler (the simplest method to find approximate solutions to first order equations) can be specified with the function deSolve::euler().↩︎